Feszültségek, ellenállások és teljesítmények háromszögei
Aki ismeri a vektordiagramokat, az könnyen észreveszi, hogy nagyon jól megkülönböztethető rajtuk egy derékszögű feszültségháromszög, amelynek minden oldala tükrözi: az áramkör teljes feszültségét, az aktív ellenállás feszültségét és a feszültséget. a reaktancián.
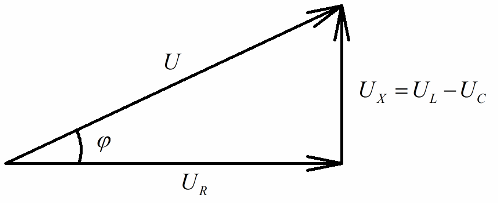
A Pitagorasz-tétellel összhangban ezeknek a feszültségeknek a kapcsolata (az áramkör teljes feszültsége és szakaszainak feszültsége között) így fog kinézni:
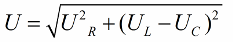
Ha a következő lépés az, hogy ezeknek a feszültségeknek az értékét elosztjuk az árammal (az áram a soros áramkör minden szakaszán egyformán halad át), akkor Ohm törvénye megkapjuk az ellenállásértékeket, vagyis most egy derékszögű ellenállási háromszögről beszélhetünk:
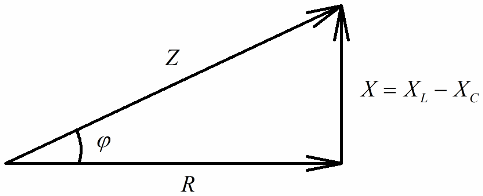
Hasonló módon (mint a feszültségek esetében) a Pitagorasz-tételt felhasználva kapcsolat létesíthető az áramkör impedanciája és a reaktanciák között. A kapcsolatot a következő képlettel fejezzük ki:
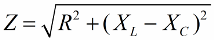
Ezután megszorozzuk az ellenállásértékeket az áramerősséggel, valójában a derékszögű háromszög mindkét oldalát bizonyos számú alkalommal növeljük. Ennek eredményeként egy derékszögű háromszöget kapunk kapacitásokkal:
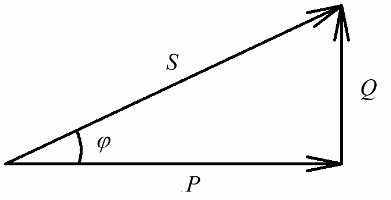
Az áramkör aktív ellenállásán felszabaduló aktív teljesítmény, amely a villamos energia visszafordíthatatlan átalakításához (hővé, a berendezésben végzett munka során) kapcsolódik, egyértelműen összefüggésben lesz a reverzibilis energiaátalakításban (a létrehozásban) szerepet játszó meddőteljesítménnyel. mágneses és elektromos mezők tekercsekben és kondenzátorokban) és teljes teljesítménnyel az elektromos rendszerhez.
Az aktív teljesítményt wattban (W), a meddőteljesítményt varis-ban (VAR - volt-amper reactive), a teljes - VA-ban (volt-amper) mérik.
A Pitagorasz-tétel szerint jogunk van írni:
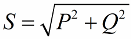
Most figyeljünk arra, hogy a hatványháromszögben van egy phi szög, melynek koszinusza elsősorban aktív és látszólagos teljesítmény alapján könnyen meghatározható. Ennek a szögnek a koszinusza (cos phi) teljesítménytényezőnek nevezzük. Megmutatja, hogy az elektromos szerelésben végzett hasznos munka során a teljes teljesítmény mekkora része kerül elszámolásra és nem kerül vissza a hálózatba.
Nyilvánvaló, hogy a nagyobb teljesítménytényező (maximum egy) az üzembe működésre szállított energia magasabb átalakítási hatásfokát jelzi. Ha a teljesítménytényező 1, akkor az összes betáplált energiát munkára használják fel.
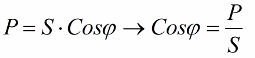
A kapott arányok lehetővé teszik a berendezés áramfelvételének kifejezését teljesítménytényezőben, aktív teljesítményben és hálózati feszültségben:
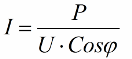
Tehát minél kisebb a koszinusz phi, annál nagyobb áramra van szüksége a hálózatnak egy bizonyos feladat elvégzéséhez. A gyakorlatban ez a tényező (maximális hálózati áram) korlátozza az átviteli vezeték átviteli kapacitását, ezért minél alacsonyabb a teljesítménytényező, annál nagyobb a vonal terhelése és annál kisebb a hasznos sávszélesség (az alacsony koszinusz phi korlátozáshoz vezet). A Joule-veszteség csökkenő koszinusz phi-vel rendelkező vezetékekben a következő képletből látható:
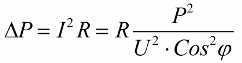
A távvezeték R aktív ellenállásán a veszteségek annál nagyobbak, minél nagyobb az I áram, pedig az reaktív a terhelésre. Ezért azt mondhatjuk, hogy alacsony teljesítménytényezővel a villamosenergia-átvitel költsége egyszerűen megnő. Ez azt jelenti, hogy a koszinusz phi növelése fontos nemzetgazdasági feladat.
Kívánatos, hogy az összteljesítmény meddő komponense megközelítse a nullát, ehhez jó lenne mindig teljes terhelésen használni a villanymotorokat, transzformátorokat, és a használat végén lekapcsolni, hogy ne járjanak alapjáraton. Terhelés nélkül a motorok és transzformátorok teljesítménytényezője nagyon alacsony. A koszinusz phi növelésének egyik módja a felhasználóknál a használata kondenzátor bankok és szinkron kompenzátorok.
