Az áramok rezonanciája

Kondenzátor és tekercs párhuzamos kapcsolása váltakozó áramú áramkörben

Tekintsük a lánc jelenségeit váltakozó árampárhuzamosan kapcsolt generátort, kondenzátort és induktort tartalmaz. Tegyük fel, hogy az áramkörnek nincs aktív ellenállása.

Nyilvánvaló, hogy egy ilyen áramkörben a tekercs és a kondenzátor feszültsége bármikor megegyezik a generátor által kifejlesztett feszültséggel.

Az áramkörben a teljes áram az ágaiban lévő áramokból áll. Az induktív ág árama a periódus negyedével elmarad a fázisfeszültségtől, a kapacitív ág árama pedig a periódus azonos negyedével vezeti le. Ezért az ágak áramai bármely pillanatban egymáshoz képest fél periódussal fáziseltoltnak bizonyulnak, azaz ellenfázisban vannak. Így az ágak áramai bármikor egymás felé irányulnak, és az áramkör el nem ágazó részében a teljes áram egyenlő a különbségükkel.

Ez jogot ad az I = IL egyenlőség -integráló áramkör felírásához

ahol én- az áramkör teljes áramának effektív értéke, I L és integrált áramkör - az ágak áramának effektív értékei.

Az Ohm törvény segítségével meghatározzuk az áram effektív értékét az ágakban, így kapjuk:

Il = U / XL és Az° C = U / XC

Ha az áramkört induktív ellenállás uralja, pl. XL Több ▼ XC, a tekercs árama kisebb, mint a kondenzátor árama; ezért az áramkör nem elágazó szakaszában az áram kapacitív jellegű, és a generátor áramköre összességében kapacitív lesz. Ezzel szemben XL-nél nagyobb XC esetén a kondenzátor árama kisebb, mint a tekercs árama; ezért az áramkör el nem ágazó szakaszában az áram induktív, és az áramkör egésze a generátor számára induktív lesz.

Nem szabad megfeledkezni arról sem, hogy a terhelés mindkét esetben reaktív, pl. az áramkör nem fogyasztja a generátor energiáját.

Az áramok rezonanciája

Tekintsük most azt az esetet, amikor a párhuzamosan kapcsolt kondenzátor és tekercs reaktanciájában egyenlőnek bizonyult, azaz. Xll = X°C.

Ha az előzőekhez hasonlóan feltételezzük, hogy a tekercsnek és a kondenzátornak nincs aktív ellenállása, akkor ha reakcióik egyenlőek (YL = Y° C), akkor az áramkör el nem ágazó részében a teljes áramerősség nulla, míg az ágakban egyenlő. az áramlatok a legnagyobb mértékben fognak folyni. Ebben az esetben a rezonanciaáramok jelensége lép fel az áramkörben.

Áramrezonancia esetén az egyes ágak áramainak effektív értékei, amelyeket az IL = U / XL és Аz° С = U / XC arányok határoznak meg, egyenlőek lesznek egymással úgy, hogy XL = XC.

A következtetés, amelyre levontunk, első pillantásra furcsának tűnhet. Valójában a generátor két ellenállással van terhelve, és az áramkör el nem ágazó részében nincs áram, miközben magukban az ellenállásokban egyenlő és ráadásul a legnagyobb áramok is áramlanak.

Ezt magyarázza a tekercs mágneses mezejének viselkedése és kondenzátor elektromos tere… Áramok rezonanciáján, mint pl feszültségrezonancia, a tekercs mezeje és a kondenzátor tere között energiaingadozás van. A generátor, miután közölte az energiát az áramkörrel, le van választva. Teljesen kikapcsolható, és az áramkör elágazó részében az áramot generátor nélkül fenntartja az az energia, amelyet az áramkör kezdetben tárol. Ezenkívül az áramkör kivezetésein a feszültség pontosan ugyanaz marad, mint a generátor által kifejlesztett feszültség.

Így az induktor és a kondenzátor párhuzamos kapcsolásakor egy olyan oszcillátor áramkört kaptunk, amely csak annyiban különbözik a fent leírtaktól, hogy a rezgéseket létrehozó generátor nincs közvetlenül az áramkörre kötve, és az áramkör zárt. 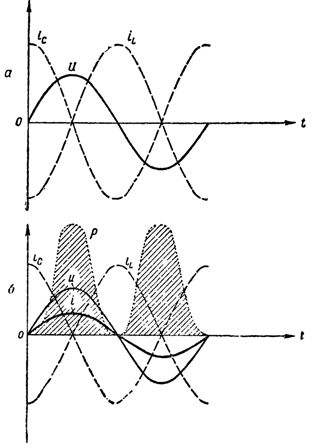Az áramkörben lévő áramok, feszültség és teljesítmény grafikonjai az áramok rezonanciája esetén: a — az aktív ellenállás nulla, az áramkör nem fogyaszt energiát; b — az áramkör aktív ellenállással rendelkezik, az áramkör el nem ágazó részében áram jelent meg, az áramkör energiát fogyaszt

L, C és e, amelynél áramrezonancia lép fel, a feszültségrezonanciához hasonlóan (ha figyelmen kívül hagyjuk az áramkör aktív ellenállását) az egyenlőség határozza meg:

ωL = 1 / ω° C

Ebből adódóan:

eres = 1/2π√LC

Lres = 1/ω2C

Darab = 1 / ω2L

E három mennyiség bármelyikének megváltoztatásával elérhető az Xl = X° C egyenlőség, azaz az áramkört oszcilláló körré alakíthatjuk.

Tehát van egy zárt oszcilláló áramkörünk, amelyben elektromos rezgéseket tudunk előidézni, pl. váltakozó áram. És ha nem lenne az az aktív ellenállás, amellyel minden rezgőkör rendelkezik, akkor folyamatosan létezhetne benne váltóáram.Az aktív ellenállás jelenléte ahhoz a tényhez vezet, hogy az áramkörben lévő rezgések fokozatosan elhalnak, és fenntartásához energiaforrásra van szükség - egy generátorra.

A nem szinuszos áramkörökben rezonancia módok lehetségesek a különböző harmonikus komponensekhez.

A gyakorlatban széles körben alkalmazzák a rezonáns áramokat. Az áramrezonancia jelenségét a sávszűrőknél elektromos "bilincsként" használják, amely késlelteti egy bizonyos frekvenciát. Mivel f frekvencián jelentős áramellenállás van, az f frekvencián a feszültségesés az áramkörben maximális lesz. A hurok ezen tulajdonságát szelektivitásnak nevezik, rádióvevőkben használják egy adott rádióállomás jelének elkülönítésére. Az áramok rezonáns üzemmódjában működő oszcilláló áramkör az egyik fő alkotóelem elektronikus generátorok.