Elektromágneses rezgések – csillapítás és kényszerrezgések nélkül

Az induktorból és a kondenzátorból álló áramkörben az elektromágneses rezgések az elektromos energia mágneses energiává történő periodikus átalakulása miatt keletkeznek, és fordítva. Ebben az esetben a kondenzátor lemezeinek elektromos töltése és a tekercsen áthaladó áram nagysága időszakosan változik.

Az elektromágneses rezgések szabadok és kényszerítettek. A szabad rezgések általában a nem nulla hurokellenállás miatt csillapodnak, a kényszerrezgések pedig általában önrezgések.

Szerez rezgőkörben szabad rezgések esetén először ki kell hoznunk ezt a rendszert az egyensúlyból: értesítsük a kondenzátort egy q0 kezdeti töltéssel, vagy valamilyen módon indítsunk el egy I0 áramimpulzust a tekercsen keresztül.

Ez egyfajta impulzusként szolgál, és szabad elektromágneses oszcillációk lépnek fel az áramkörben - megkezdődik a kondenzátor váltakozó feltöltésének és kisütésének folyamata az induktív tekercsen keresztül, és ennek megfelelően a tekercs mágneses mezőjének változó emelkedése és süllyedése.

Azokat az oszcillációkat, amelyeket egy áramkörben külső váltakozó elektromotoros erő tart fenn, kényszerrezgéseknek nevezzük. Tehát, amint már megértette, a legegyszerűbb oszcilláló rendszer példája, amelyben szabad elektromágneses rezgések figyelhetők meg, egy rezgőkör, amely egy C elektromos kapacitású kondenzátorból és egy L induktivitású tekercsből áll.

Valódi oszcillációs körben a kondenzátor újratöltési folyamata periodikusan megismétlődik, de a rezgések gyorsan elhalnak, mert az energia főként a tekercshuzal aktív ellenállásán R disszipálódik.

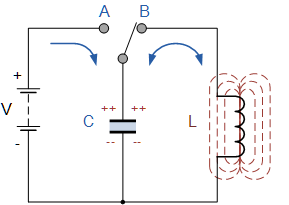
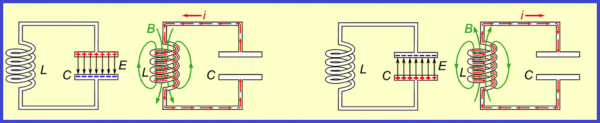
Tekintsünk egy ideális oszcilláló áramkört. Először töltsük fel a kondenzátort az akkumulátorról - adjuk neki a kezdeti töltést q0, vagyis feltöltjük energiával a kondenzátort. Ez lesz a We kondenzátor maximális energiája.

Következő lépésként le kell választani a kondenzátort az akkumulátorról, és az induktorral párhuzamosan csatlakoztatni. Ezen a ponton a kondenzátor kisülni kezd, és a tekercs áramkörében növekvő áram jelenik meg. Minél hosszabb ideig kisül a kondenzátor, annál több töltés jut belőle fokozatosan a tekercsbe, annál nagyobb lesz a tekercsben lévő áram, így a tekercs mágneses tér formájában tárolja az energiát.

Ez a folyamat nem azonnal, hanem fokozatosan megy végbe, mivel a tekercsnek van induktivitása, ami azt jelenti, hogy fellép az önindukció jelensége, ami abban áll, hogy a tekercs egyébként is ellenáll az áram növekedésének. Egy ponton a tekercs mágneses mező energiája eléri a lehetséges maximális Wm értéket (attól függően, hogy kezdetben mekkora töltést vittek át a kondenzátorba, és mekkora az áramkör ellenállása).

Ezenkívül az önindukció jelensége miatt a tekercsen áthaladó áram ugyanabban az irányban marad, de a nagysága csökken, és az elektromos töltés végül ismét felhalmozódik a kondenzátorban. Ily módon a kondenzátor újratöltődik. A lemezei most ellentétes töltési előjelűek, mint a kísérlet elején, amikor a kondenzátort csatlakoztattuk az akkumulátorhoz.

A kondenzátor energiája elérte a lehetséges maximális értéket ennél az áramkörnél. Az áramkörben leállt az áram. Most a folyamat az ellenkező irányba indul el, és ez újra és újra folytatódni fog, vagyis szabad elektromágneses rezgések lesznek.

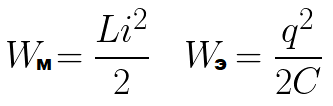
Ha az R áramkör aktív ellenállása nulla, akkor a kondenzátorlapokon áthaladó feszültség és a tekercsen áthaladó áram végtelenül változik a harmonikus törvény szerint - koszinusz vagy szinusz. Ezt hívják harmonikus rezgésnek. A kondenzátorlapok töltése is egy harmonikus törvény szerint változna.

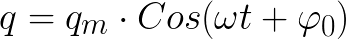
Az ideális ciklusban nincs veszteség. És ha így lenne, akkor az áramkörben a szabad rezgések időtartama csak a kondenzátor C kapacitásának és a tekercs L induktivitásának értékétől függne. Ez a periódus megtalálható (az ideális ciklushoz, ahol R = 0) a Thomson-képlet segítségével:

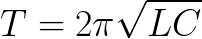
A megfelelő frekvencia és ciklusfrekvencia egy ideális veszteségmentes áramkörhöz a következő képletekkel található:

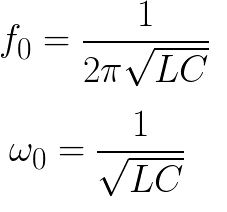
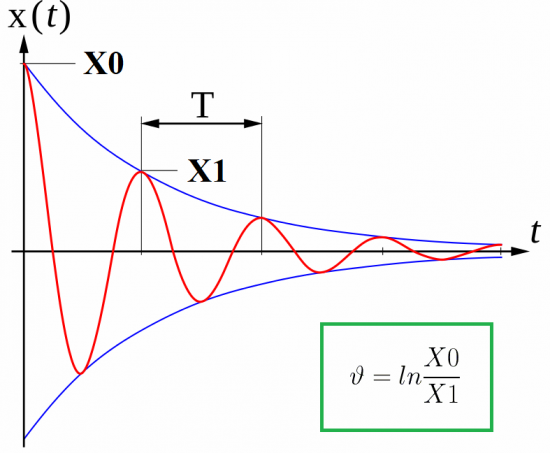
Ideális áramkörök azonban nem léteznek, és az elektromágneses oszcilláció csillapodik a vezetékek felmelegedése miatti veszteségek miatt. Az R áramköri ellenállás értékétől függően minden további maximális kondenzátorfeszültség alacsonyabb lesz, mint az előző.

Ezzel a jelenséggel kapcsolatban olyan paramétert vezetnek be a fizikában, mint az oszcillációk logaritmikus csökkenése vagy a csillapítási csökkenés. Megállapítható, hogy az oszcillációk két egymást követő maximuma (azonos előjelű) arányának természetes logaritmusa:

A logaritmikus oszcilláció-csökkentés az ideális rezgési periódushoz kapcsolódik a következő összefüggéssel, ahol további paraméter is bevezethető, az ún. Csillapítási tényező:

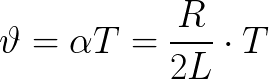
A csillapítás befolyásolja a szabad rezgések frekvenciáját. Ezért a szabad csillapított rezgések frekvenciájának meghatározására szolgáló képlet egy valós oszcilláló áramkörben eltér az ideális áramkör képletétől (a csillapítási tényezőt figyelembe veszik):

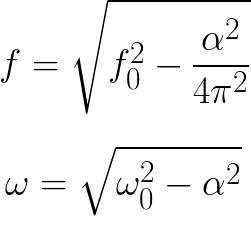
Lengések létrehozására az áramkörben feloldva, ezeket a veszteségeket félperiódusonként pótolni és kompenzálni kell. Ezt a folyamatos oszcillációs generátorokban érik el, ahol a külső EMF-forrás energiájával kompenzálja a hőveszteséget. Az ilyen rezgésrendszert külső EMF-forrással önoszcillálónak nevezzük.