Az áram és a feszültség RMS értékei
A váltakozó szinuszos áramnak különböző pillanatnyi értékei vannak az időszak alatt. Természetes a kérdés, hogy az áramkörben lévő ampermérővel mekkora áramerősséget mérünk?
A váltakozó áramú áramkörök, valamint az elektromos mérések kiszámításakor kényelmetlen az áramok és feszültségek pillanatnyi vagy amplitúdóértékeit használni, és ezek átlagos értéke egy időszak alatt nulla. Ráadásul egy periodikusan változó áram elektromos hatása (a felszabaduló hőmennyiség, a tökéletes működés stb.) ennek az áramnak az amplitúdójával nem becsülhető meg.
A legkényelmesebb az áram és a feszültség úgynevezett effektív értékeinek fogalmának bevezetése volt... Ezek a fogalmak az áram termikus (vagy mechanikai) hatásán alapulnak, amely nem függ az áram irányától.
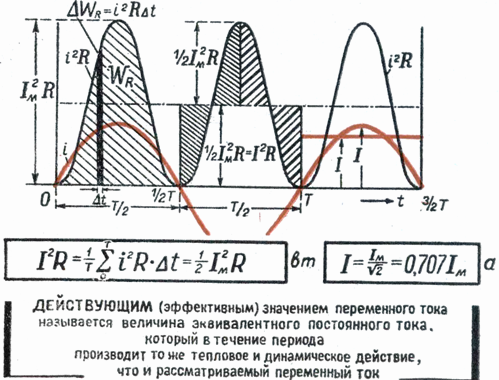
A váltakozó áram négyzetes középértéke - ez az egyenáram azon értéke, amelynél a váltakozó áram időtartama alatt ugyanolyan mennyiségű hő szabadul fel a vezetőben, mint a váltakozó áram alatt.
A megtett intézkedések értékelésére váltakozó áramHatásait összevetjük az egyenáram termikus hatásával.
Az r ellenálláson áthaladó P egyenáram P = P2r lesz.
A váltakozó áramú teljesítményt az Az2r pillanatnyi teljesítmény átlagos hatásaként fejezzük ki a teljes periódusra, vagy (I am x sinωT)2 NS r átlagaként ugyanarra az időre.
Legyen a periódusra vonatkozó t2 átlagértéke M. Az egyenáram és a váltóáram teljesítményét egyenlővé téve a következőt kapjuk: Az2r = Mr -n, ahonnan Az = √M,
Az I mennyiséget a váltakozó áram effektív értékének nevezzük.
Az i2 átlagos értékét váltakozó áramon a következőképpen határozzuk meg.
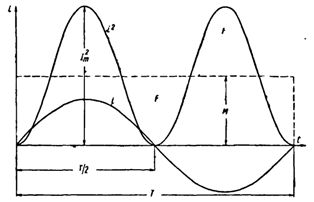
Készítsünk szinuszos áramgörbét. Az egyes pillanatnyi áramértékek négyzetre emelésével P-idő görbét kapunk.
AC effektív érték
Ennek a görbének mindkét fele a vízszintes tengely felett van, mivel a periódus második felében a negatív áramok (-i) négyzetre vetve pozitív értékeket adnak.
Szerkesszünk olyan téglalapot, amelynek T alapja és területe egyenlő az i2 görbe és a vízszintes tengely által határolt területtel. Az M téglalap magassága megfelel a periódus P átlagos értékének. Ez a periódusérték a magasabb matematikával számolva 1/2 I2m lesz... Ezért M. = 1/2 I2m
Mivel az Im váltóáram effektív érték Im = √M, akkor végül I = Im / √2
Hasonlóképpen, az U és E feszültség effektív értéke és amplitúdója közötti kapcsolat a következőképpen alakul:
U = Um / √2E = Em / √2
A változók effektív értékeit nagybetűk jelzik alsó indexek nélkül (I, U, E).
A fentiek alapján azt mondhatjuk, hogy a váltóáram effektív értéke megegyezik egy olyan egyenárammal, amely a váltakozó árammal azonos ellenálláson áthaladva egyidejűleg ugyanannyi energiát szabadít fel.
A váltakozó áramú áramkörbe tartozó elektromos mérőműszerek (ampermérők, voltmérők) jelzik az áram vagy a feszültség effektív értékeit.
A vektordiagramok készítésekor kényelmesebb nem az amplitúdót, hanem a vektorok effektív értékeit elhalasztani. Ehhez a vektorok hosszát egyszer √2-vel csökkentjük. Ez nem változtatja meg a vektorok helyét a diagramon.