Hogyan kell kiszámítani az induktivitást
Ahogy a mechanikában egy tömeggel rendelkező test ellenáll a gyorsulásnak a térben, tehetetlenséget nyilvánítva, úgy az induktivitás megakadályozza, hogy a vezetőben az áram megváltozzon, önindukciós EMF-t hozva létre. Ez az önindukció EMF-je, amely egyszerre ellenzi az áram csökkenését, megpróbálva fenntartani, és az áram növekedését, megpróbálva csökkenteni.
Az a tény, hogy az áramkörben lévő áram megváltoztatása (növelése vagy csökkentése) folyamatában az áram által létrehozott mágneses fluxus is megváltozik, amely főleg az áramkör által korlátozott területen lokalizálódik. És ahogy a mágneses fluxus növekszik vagy csökken, önindukciós EMF-et indukál (Lenz szabálya szerint - az ezt okozó ok, vagyis az elején említett áram ellen), mindezt ugyanabban az áramkörben. Az L induktivitást itt az I áram és a Φ teljes mágneses fluxus közötti arányossági tényezőnek nevezzük, ezt az áramot a következők generálják:
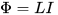
Tehát minél nagyobb az áramkör induktivitása, annál erősebb, mint a keletkező mágneses tér, megakadályozza az áram változását (ez a mező hozza létre), ezért hosszabb ideig tart, amíg az áram nagyobb induktivitáson keresztül változik, azonos alkalmazott feszültséggel. A következő állítás is igaz: minél nagyobb az induktivitás, annál nagyobb lesz a feszültség az áramkörön, amikor a mágneses fluxus megváltozik.

Tegyük fel, hogy egy bizonyos tartományban állandó sebességgel változtatjuk a mágneses fluxust, akkor ezt a tartományt különböző áramkörökkel lefedve több feszültséget kapunk azon az áramkörön, amelynek nagyobb az induktivitása (transzformátor, Rumkorf tekercs stb. ezen az elven működik).
De hogyan számítják ki a hurok induktivitását? Hogyan lehet megtalálni az arányossági tényezőt az áram és a mágneses fluxus között? Az első dolog, amit meg kell jegyeznünk, hogy az induktivitás változik a Henry-ben (H). Az 1 henry induktivitású áramkör kivezetésein, ha az áramerősség másodpercenként egy amperrel változik, 1 voltos feszültség jelenik meg.
Az induktivitás nagysága két paramétertől függ: az áramkör geometriai méreteitől (hossz, szélesség, fordulatok száma stb.) és a közeg mágneses tulajdonságaitól (ha pl. tekercs, az induktivitása nagyobb lesz, mint ha nincs benne mag).
A keletkező induktivitás kiszámításához tudnia kell, hogy maga a tekercs milyen alakú lesz, és milyen mágneses permeabilitással rendelkezik a benne lévő közeg (a közeg relatív mágneses permeabilitása a vákuum mágneses permeabilitása és a mágneses áteresztőképesség arányossági tényezője adott közeg permeabilitása.Természetesen a különböző anyagoknál eltérő)…
Nézzük meg a tekercsek leggyakoribb formáinak (hengeres mágnesszelep, toroid és hosszú huzal) induktivitásának kiszámítására szolgáló képleteket.
Itt van az induktivitás kiszámításának képlete szolenoid — tekercsek, amelyek hossza jóval nagyobb, mint az átmérő:
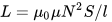
Mint látható, ismerve az N fordulatok számát, az l tekercs hosszát és az S tekercs keresztmetszeti területét, megkapjuk a tekercs hozzávetőleges induktivitását mag nélkül vagy maggal, míg a mágneses A vákuum permeabilitása állandó érték:
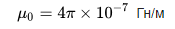
A toroid tekercs induktivitása, ahol h a toroid magassága, r a toroid belső átmérője, R a toroid külső átmérője:
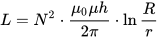
Egy vékony vezeték induktivitása (a keresztmetszet sugara sokkal kisebb, mint a hossz), ahol l a vezeték hossza, r pedig a keresztmetszet sugara. Mu i és e indexekkel a a belső (belső, vezető anyagok) és a külső (külső, vezetőn kívüli anyagok) környezet relatív mágneses permeabilitása:
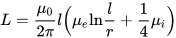
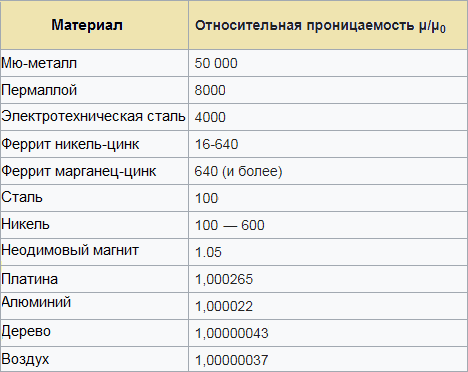
A relatív permittivitások táblázata segít megbecsülni, hogy mekkora induktivitás várható egy bizonyos mágneses anyagot magként használó áramkörtől (huzal, tekercs):