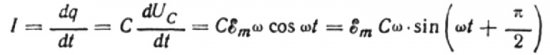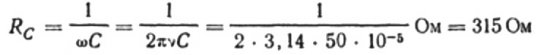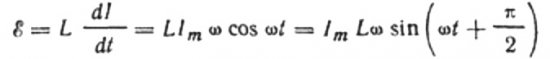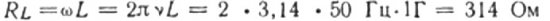Kapacitív és induktív ellenállás váltakozó áramú áramkörben

Ha egy kondenzátort is beépítünk egy egyenáramú áramkörbe, akkor azt találjuk, hogy annak végtelen az ellenállása, mert az egyenáram egyszerűen nem tud áthaladni a lemezek közötti dielektrikumon, mivel a dielektrikum definíció szerint nem vezet egyenáramot.

Egy kondenzátor megszakítja az egyenáramú áramkört. De ha ugyanaz a kondenzátor most benne van a váltakozó áramkörben, akkor kiderül, hogy a kondenzátora úgy tűnik, hogy nem törik meg teljesen, egyszerűen váltakozik és töltődik, vagyis az elektromos töltés mozog, és a külső áramkörben lévő áram fenntartott.

Maxwell elmélete alapján ebben az esetben azt mondhatjuk, hogy a kondenzátoron belüli váltakozó vezetési áram továbbra is zárva van, csak ebben az esetben - az előfeszítő áram miatt. Ez azt jelenti, hogy az AC áramkörben lévő kondenzátor véges értékű ellenállásként működik. Ezt az ellenállást ún kapacitív.

A gyakorlat régóta bebizonyította, hogy a vezetőn átfolyó váltakozó áram mennyisége a vezető alakjától és a körülötte lévő közeg mágneses tulajdonságaitól függ.Egyenes vezetéknél az áramerősség a legnagyobb, és ha ugyanazt a vezetéket egy nagy fordulatszámú tekercsbe tekerjük, az áram kisebb lesz.

És ha ugyanabba a tekercsbe ferromágneses magot vezetnek be, az áramerősség még jobban csökken. Ezért a vezeték nem csak ohmos (aktív) ellenállással, hanem a vezeték induktivitásának függvényében további ellenállással is biztosít váltakozó áramot.Ezt az ellenállást ún. induktív.

Fizikai jelentése az, hogy egy bizonyos induktivitású vezetőben a változó áram önindukciós EMF-et indít el abban a vezetőben, amely megakadályozza az áram változását, vagyis csökkenti az áramerősséget. Ez egyenértékű a vezeték ellenállásának növelésével.

Kapacitás az AC áramkörben

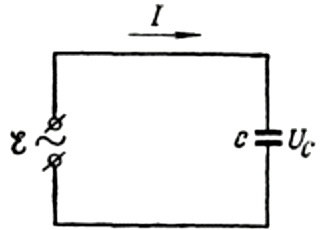
Először is beszéljünk részletesebben a kapacitív ellenállásról. Tegyük fel, hogy egy C kapacitású kondenzátor egy szinuszos váltakozó áramforráshoz van csatlakoztatva, akkor ennek a forrásnak az EMF-jét a következő képlettel írjuk le:

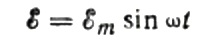
Figyelmen kívül hagyjuk a csatlakozó vezetékek feszültségesését, mivel az általában nagyon kicsi, és szükség esetén külön is figyelembe vehető. Tegyük fel most, hogy a kondenzátorlapokon a feszültség megegyezik a váltakozó áramú forrás feszültségével. Akkor:

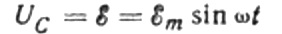
Egy adott pillanatban a kondenzátor töltése a kapacitásától és a lemezei közötti feszültségtől függ. Ezután a fent említett ismert forrás ismeretében egy kifejezést kapunk a kondenzátorlemezek töltésének meghatározására a forrásfeszültség alapján:

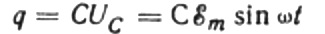
Hagyjuk, hogy dt végtelen ideig a kondenzátor töltése dq-val megváltozik, ekkor a forrástól a kondenzátorig terjedő vezetékeken I áram fog átfolyni, ami egyenlő:

Az áram amplitúdójának értéke egyenlő lesz:

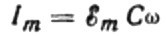
Ekkor az áram végső kifejezése a következő lesz:

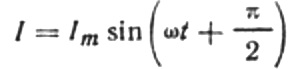
Írjuk át az aktuális amplitúdó képletét a következőképpen:

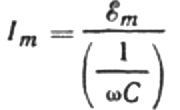
Ez az arány az Ohm-törvény, ahol a szögfrekvencia és a kapacitás szorzatának reciprokja játssza az ellenállás szerepét, és valójában egy kifejezés egy kondenzátor kapacitásának meghatározására szinuszos váltóáramú áramkörben:

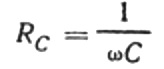
Ez azt jelenti, hogy a kapacitív ellenállás fordítottan arányos az áram szögfrekvenciájával és a kondenzátor kapacitásával. Könnyű megérteni ennek a függőségnek a fizikai jelentését.

Minél nagyobb a kondenzátor kapacitása az AC áramkörben, és minél gyakrabban változik az áram iránya ebben az áramkörben, végső soron több teljes töltés halad át egységnyi idő alatt a kondenzátort a váltakozó áramú forrással összekötő vezetékek keresztmetszetén. Ez azt jelenti, hogy az áramerősség arányos a kapacitás és a szögfrekvencia szorzatával.

Például számítsuk ki egy 10 mikrofarad elektromos kapacitású kondenzátor kapacitását egy 50 Hz frekvenciájú szinuszos váltakozó áramú áramkörhöz:

Ha a frekvencia 5000 Hz lenne, akkor ugyanaz a kondenzátor körülbelül 3 ohm ellenállást mutatna.

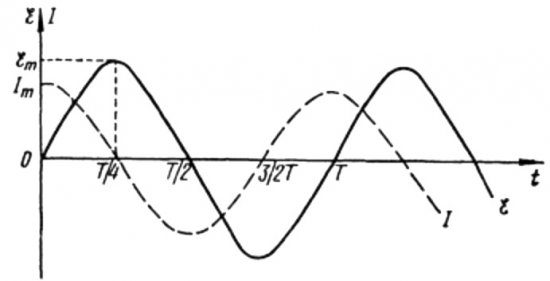
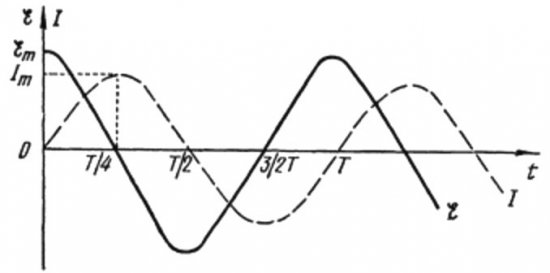
A fenti képletekből jól látható, hogy a kondenzátoros váltakozó áramú áramkörben az áram és a feszültség mindig különböző fázisokban változik. Az áramfázis pi / 2-vel (90 fokkal) vezeti a feszültség fázist. Ez azt jelenti, hogy a maximális áramerősség időben mindig egy negyed periódussal korábban létezik, mint a maximális feszültség. Így a kapacitív ellenálláson keresztül az áram az időtartam negyedével, vagy fázisban 90 fokkal vezeti a feszültséget.

Magyarázzuk meg ennek a jelenségnek a fizikai jelentését.Az első pillanatban a kondenzátor teljesen lemerül, így a rákapcsolt legkisebb feszültség már megmozgatja a töltéseket a kondenzátor lemezein, áramot hozva létre.

Ahogy a kondenzátor töltődik, a lemezein lévő feszültség növekszik, ez megakadályozza a töltés további áramlását, így az áramkörben az áram a lemezekre adott feszültség további növekedése ellenére csökken.

Ez azt jelenti, hogy ha a kezdeti pillanatban az áramerősség maximális volt, akkor amikor a feszültség negyed periódus után eléri a maximumot, az áram teljesen leáll.

A periódus elején az áramerősség maximális, a feszültség pedig minimális és elkezd növekedni, de a periódus negyede után a feszültség eléri a maximumot, de az áram ekkorra már nullára süllyedt. Így kiderül, hogy a feszültség a periódus negyedével vezeti a feszültséget.

AC induktív ellenállás

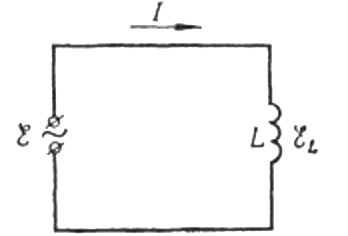
Most térjünk vissza az induktív ellenálláshoz. Tegyük fel, hogy egy induktivitású tekercsen szinuszos váltakozó áram folyik át. A következőképpen fejezhető ki:

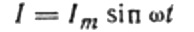
Az áramot a tekercsre adott váltakozó feszültség okozza. Ez azt jelenti, hogy egy önindukciós EMF jelenik meg a tekercsen, ami a következőképpen fejeződik ki:

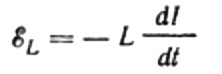
Ismét figyelmen kívül hagyjuk a feszültségesést az EMF-forrást a tekercshez csatlakozó vezetékeken. Ohmos ellenállásuk nagyon alacsony.

A tekercsre adott váltakozó feszültséget minden pillanatban teljesen kiegyenlítse a vele egyenlő nagyságú, de ellentétes irányú önindukciós EMF:

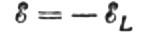
Akkor jogunk van írni:

Mivel a tekercsre adott feszültség amplitúdója:

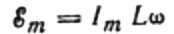
kapunk:

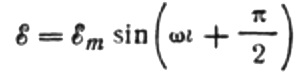
Adjuk meg a maximális áramerősséget a következőképpen:

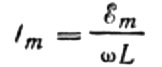
Ez a kifejezés lényegében Ohm törvénye. Az induktivitás és a szögfrekvencia szorzatával egyenlő mennyiség játszik itt ellenállás szerepet, és nem más, mint az induktivitás induktív ellenállása:

Tehát az induktív ellenállás arányos a tekercs induktivitásával és a tekercsen áthaladó váltakozó áram szögfrekvenciájával.

Ez annak a ténynek köszönhető, hogy az induktív ellenállás az önindukciós EMF-nek a forrásfeszültségre gyakorolt ​​hatásának köszönhető, - az önindukciós EMF csökkenti az áramerősséget, és ezért ellenállást hoz az áramkörben. Az önindukció emf nagysága, mint ismeretes, arányos a tekercs induktivitásával és a rajta áthaladó áram változási sebességével.

Például számítsuk ki egy 1 H induktivitású tekercs induktív ellenállását, amely egy 50 Hz áramfrekvenciájú áramkörben található:

Ha a golyó frekvenciája 5000 Hz lenne, akkor ugyanannak a tekercsnek az ellenállása hozzávetőlegesen 31 400 ohm lenne.. Emlékezzünk vissza, hogy a tekercsvezeték ohmos ellenállása általában néhány ohm.

A fenti képletekből nyilvánvaló, hogy a tekercsen átmenő áram és a benne lévő feszültség változásai különböző fázisokban fordulnak elő, és az áram fázisa mindig kisebb, mint a pi / 2 feszültség fázisa. a maximális áramerősség negyed periódussal később következik be, mint a maximális feszültség kezdete.

Az induktív ellenállásban az áram az önindukált EMF fékező hatása miatt 90 fokkal lemarad a feszültségtől, ami megakadályozza az áram változását (mind a növekedését, mind a csökkenését), így a tekercses áramkörben később a maximális áramerősség figyelhető meg. mint a maximális feszültség.

Tekercs és kondenzátor kombinált hatás

Ha egy kondenzátoros tekercset sorba kötünk egy váltóáramú áramkörrel, akkor a tekercs feszültsége a kondenzátor feszültségét időben fél periódussal, azaz fázisban 180 fokkal megnöveli.

A kapacitív és induktív ellenállást ún reagensek… Az energiát nem a reaktív ellenállás, hanem az aktív ellenállás költi el. A kondenzátorban tárolt energia periodikusan visszakerül a forrásba, amikor a kondenzátorban lévő elektromos mező eltűnik.

Ugyanígy van ez a tekercsnél is: mivel a tekercs mágneses terét az áram hozza létre, a benne lévő energia a periódus egynegyede alatt felhalmozódik, majd a periódus következő negyedében visszatér a forráshoz. Ebben a cikkben a szinuszos váltóáramról beszéltünk, amelyre ezeket az előírásokat szigorúan betartják.

A váltakozó áramú szinuszos áramkörökben a magos tekercseket ún fullasztóhagyományosan áramkorlátozásra használják. Előnyük a reosztátokkal szemben, hogy az energia nem oszlik el hatalmas mennyiségben hőként.