Aszinkron motoros működés

Az indukciós motor működése grafikusan kifejezve az n2 fordulatszám, az η hatásfok, az M2 hasznos nyomaték (tengelynyomaték), a cos φ teljesítménytényező és az állórészáram I1 függése a P2 hasznos teljesítménytől U1 = const f1 = const.

Sebességkarakterisztika n2 = f (P2). Az indukciós motor forgórészének fordulatszáma n2 = n1 (1 — s).

Slide s = Pe2 / Rem, azaz. az indukciós motor csúszását és így a fordulatszámát a forgórész elektromos veszteségének az elektromágneses teljesítményhez viszonyított aránya határozza meg. Az üresjárati forgórész elektromos veszteségeit figyelmen kívül hagyva Pe2 = 0-t vehetünk fel, ezért s ≈ 0 és n20 ≈ n1.

A tengelyterhelés növekedésével aszinkron motor az s = Pe2 / Pem arány növekszik, névleges terhelésnél elérve a 0,01-0,08 értéket. Ennek megfelelően az n2 = f (P2) függés az abszcissza tengelyéhez képest enyhén ferde görbe. Azonban ahogy a motor rotor aktív ellenállása r2 ' növekszik, a görbe meredeksége nő. Ebben az esetben az indukciós motor n2 frekvenciájának változása a P2 terhelés ingadozásával együtt nő.Ez azzal magyarázható, hogy az r2 ' növekedésével a forgórész elektromos veszteségei nőnek.

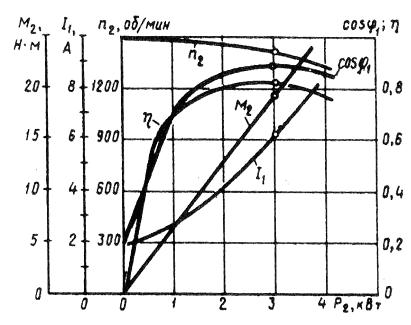
Rizs. 1. Az indukciós motor működési jellemzői

Függőség M2 = f (P2). Az M2 aszinkron motor tengelyétől származó hasznos nyomaték P2 hasznos teljesítménytől való függését az M2 = P2 / ω2 = 60 P2 / (2πn2) = 9,55P2 / n2 kifejezés határozza meg,

ahol P2 – hasznos teljesítmény, W; ω2 = 2πf 2/60 a forgórész forgási szögfrekvenciája.

Ebből a kifejezésből következik, hogy ha n2 = const, akkor az M2 = f2 (P2) gráf egy egyenes. De a P2 terhelés növekedésével járó indukciós motorban a forgórész fordulatszáma csökken, ezért az M2 tengely hasznos nyomatéka a terhelés növekedésével egy kicsit gyorsabban növekszik, mint a terhelés, ezért az M2 = f grafikon (P2) ) görbe alakja van.

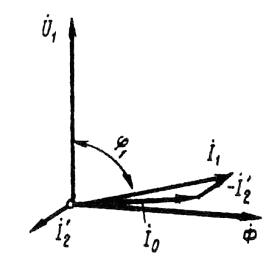Rizs. 2. Kis terhelésű indukciós motor vektordiagramja

Függőség cos φ1 = f (P2). Tekintettel arra, hogy az I1 indukciós motor állórészáramának van egy reaktív (induktív) komponense, amely szükséges az állórészben mágneses tér létrehozásához, az aszinkronmotorok teljesítménytényezője egységnyinél kisebb. A teljesítménytényező legalacsonyabb értéke az alapjáratnak felel meg. Ez azzal magyarázható, hogy az I0 villanymotor üresjárati árama bármilyen terhelésnél gyakorlatilag változatlan marad. Ezért kis motorterhelésnél az állórész árama kicsi és nagyrészt reaktív (I1 ≈ I0). Ennek eredményeként az állórész áramának fáziseltolása a feszültséghez képest jelentős (φ1 ≈ φ0), csak valamivel kevesebb, mint 90 ° (2. ábra).

Az indukciós motorok üresjárati teljesítménytényezője általában 0,2-nél kisebb.A motortengely terhelésének növekedésével az I1 áram aktív komponense növekszik, és a teljesítménytényező növekszik, és a névlegeshez közeli terhelésnél éri el a legmagasabb értéket (0,80 - 0,90). A motortengely terhelésének további növekedését a cos φ1 csökkenése kíséri, ami a forgórész induktív ellenállásának (x2s) növekedésével magyarázható a csúszás és ezáltal a forgórész frekvenciájának növekedése miatt. az áram a rotorban.

Az indukciós motorok teljesítménytényezőjének javítása érdekében rendkívül fontos, hogy a motor mindig, vagy legalább az idő jelentős részében a névleges terheléshez közeli terheléssel járjon. Ez csak a motorteljesítmény helyes megválasztásával érhető el. Ha a motor az idő jelentős részében terhelés alatt működik, akkor a cos φ1 növeléséhez célszerű csökkenteni a motorra táplált U1 feszültséget. Például az állórész-tekercselés delta-kapcsolása mellett működő motoroknál ezt úgy lehet megtenni, hogy az állórész tekercseit csillagba kapcsolják, ami a fázisfeszültség egy faktoros csökkenését okozza. Ebben az esetben az állórész mágneses fluxusa, és így a mágnesező áram körülbelül egy tényezővel csökken. Ezenkívül az állórész áramának aktív összetevője kissé megnő. Mindez hozzájárul a motor teljesítménytényezőjének növeléséhez.

ábrán. A 3. ábra a cos φ1, aszinkron motor terheléstől való függésének grafikonját mutatja, ha az állórész tekercseit csillagban (1. görbe) és delta (2. görbe) köti össze.

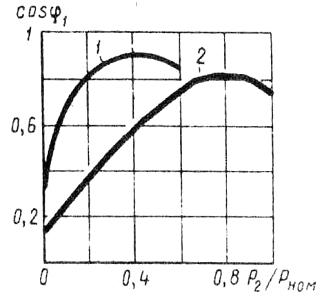
Rizs. 3. A cos φ1 terheléstől való függése a motor állórész tekercsének csillaggal (1) és delta (2) való csatlakoztatásakor