Feszültségesés

Fogalmak és képletek

Minden r ellenállásnál, amikor az I áram áthalad, megjelenik egy U = I ∙ r feszültség, amelyet általában ezen ellenállás feszültségesésének neveznek.

Ha csak egy r ellenállás van az áramkörben, akkor a teljes Ust forrásfeszültség erre az ellenállásra esik.

Ha az áramkörben két r1 és r2 ellenállás van sorba kötve, akkor az U1 = I ∙ r1 és U2 = I ∙ r2 ellenállások feszültségeinek összege, azaz. feszültségesés megegyezik a forrásfeszültséggel: Ust = U1 + U2.

A tápfeszültség egyenlő az áramkör feszültségesésének összegével (Kirchhoff 2. törvénye).

Példák

1. Mekkora feszültségesés következik be az r = 15 Ohm ellenállású lámpa izzószálán, amikor az I = 0,3 A áram áthalad (1. ábra)?

Rizs. 1.

A feszültségesések száma Ohm törvénye: U = I ∙ r = 0,3 ∙ 15 = 4,5 V.

A lámpa 1. és 2. pontja között (lásd az ábrát) a feszültség 4,5 V. A lámpa akkor világít rendesen, ha névleges áram folyik rajta, vagy ha névleges feszültség van az 1. és 2. pont között (a névleges áram és feszültség látható a lámpán).

2. Két egyforma, 2,5 V feszültségű és 0,3 A áramerősségű izzót sorba kapcsolunk, és egy 4,5 V feszültségű zsebakkumulátorra csatlakoztatjuk. Milyen feszültségesés keletkezik az egyes izzók kapcsain (2. ábra). ) ) ?

Rizs. 2.

Az azonos izzók ellenállása azonos r. Sorba kapcsolva ugyanaz az I áram folyik át rajtuk. Ebből következik, hogy ugyanolyan feszültségesések lesznek, ezen feszültségek összegének meg kell egyeznie az U = 4,5 V forrásfeszültséggel. Mindegyik izzó feszültsége 4 , 5: 2 = 2,25 V.

Megoldhatja ezt a problémát és a szekvenciális számítást. Az izzó ellenállását az adatok alapján számítjuk ki: rl = 2,5 / 0,3 = 8,33 Ohm.

I. áramköri áram = U / (2rl) = 4,5 / 16,66 = 0,27 A.

A feszültségesés az izzón U = Irl = 0,27 ∙ 8,33 = 2,25 V.

3. A sín és a villamosvonal felsővezetéke közötti feszültség 500 V. A világításhoz négy egyforma, sorba kapcsolt lámpa szolgál. Milyen feszültségre kell kiválasztani az egyes lámpákat (3. ábra)?

Rizs. 3.

Az azonos lámpáknak egyenlő ellenállásuk van, amelyeken ugyanaz az áram folyik át. A lámpák feszültségesése is azonos lesz. Ez azt jelenti, hogy minden lámpánál 500 lesz: 4 = 125 V.

4. Két 40 és 60 W teljesítményű, 220 V névleges feszültségű lámpát sorba kapcsolunk, és 220 V feszültségű hálózatba kapcsoljuk. Milyen feszültségesés következik be mindegyiken (4. ábra)?

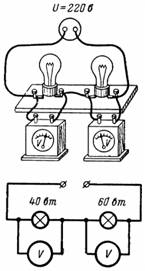
Rizs. 4.

Az első lámpa ellenállása r1 = 1210 Ohm, a második r2 = 806,6 Ohm (fűtött állapotban). A lámpákon áthaladó áram I = U / (r1 + r2) = 220 / 2016,6 = 0,109 A.

Feszültségesés az első lámpában U1 = I ∙ r1 = 0,109 ∙ 1210 = 132 V.

Feszültségesés a második lámpában U2 = I ∙ r2 = 0,109 ∙ 806,6 = 88 V.

A nagyobb ellenállású lámpáknál nagyobb a feszültségesés és fordítva. Mindkét lámpa izzószála nagyon gyenge, de a 40 W-os lámpa valamivel erősebb, mint a 60 W-os.

5. Ahhoz, hogy a D villanymotor feszültsége (5. ábra) 220 V legyen, a hosszú vezeték elején (az erőműnél) a feszültségnek 220 V-nál nagyobbnak kell lennie. feszültségesés (veszteség) online. Minél nagyobb a vezeték ellenállása és a benne lévő áram, annál nagyobb a feszültségesés a vonal mentén.

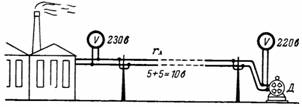Rizs. 5.

Példánkban a vezeték minden vezetékében a feszültségesés 5 V. Ekkor az erőmű gyűjtősínein a feszültségnek 230 V-nak kell lennie.

6. A fogyasztót 80 V-os, 30 A áramerősségű akkumulátor táplálja. A fogyasztó normál működéséhez a 16 mm2 keresztmetszetű alumínium vezetékekben 3%-os feszültségesés megengedett. Mekkora a maximális távolság az akkumulátor és a felhasználó között?

Megengedett feszültségesés a vezetékben U = 3/100 ∙ 80 = 2,4 V.

A vezetékek ellenállását a megengedett feszültségesés rpr = U / I = 2,4 / 30 = 0,08 Ohm korlátozza.

Az ellenállás meghatározására szolgáló képlet segítségével kiszámítjuk a vezetékek hosszát: r = ρ ∙ l / S, ahonnan l = (r ∙ S) / ρ = (0,08 ∙ 16) / 0,029 = 44,1 m.

Ha a felhasználó 22 ​​m-re van az akkumulátortól, akkor a benne lévő feszültség 3%-nál kisebb lesz, mint 80 V, azaz. egyenlő 77,6 V.

7. 20 km hosszú távíróvezeték 3,5 mm átmérőjű acélhuzalból készül. A visszatérő vezetéket fémsíneken keresztüli földelés váltja fel. A busz és a test közötti átmenet ellenállása rz = 50 Ohm.Mekkora legyen az akkumulátor feszültsége a vezeték elején, ha a vezeték végén lévő relé ellenállása рп = 300 Ohm és a relé árama I = 5 mA?

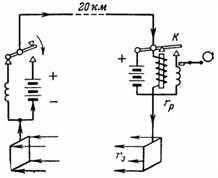
Rizs. 6.

A kapcsolási rajz az ábrán látható. 6. Ha a távíró kapcsolót a jel küldési pontján megnyomjuk, a vonal végén lévő vételi ponton lévő relé magához vonzza a K armatúrát, amely viszont az érintkezőjével bekapcsolja a rögzítő tekercsét. A kimeneti feszültségnek kompenzálnia kell a vezeték feszültségesését, a vevőrelét és a földelő gyűjtősínek tranziens ellenállásait: U = I ∙ rl + I ∙ rр + I ∙ 2 ∙ rр; U = I ∙ (rр + рр + 2 ∙ rр).

A forrásfeszültség egyenlő az áramerősség és az áramkör teljes ellenállásának szorzatával.

A vezeték keresztmetszete S = (π ∙ d ^ 2) / 4 = (π ∙ 3,5 ^ 2) / 4 = 9,6 mm2.

Vonalellenállás rl = ρ ∙ l / S = 0,11 ∙ 20 000 / 9,6 = 229,2 ohm.

Az eredő ellenállás r = 229,2 + 300 + 2 ∙ 50 = 629,2 Ohm.

Kimeneti feszültség U = I ∙ r = 0,005 ∙ 629,2 = 3,146 V; U≈3,2 V.

A vezeték feszültségesése I = 0,005 A áram áthaladásakor a következő lesz: Ul = I ∙ rl = 0,005 ∙ 229,2 = 1,146 V.

A viszonylag kis feszültségesést a vezetékben az áram alacsony értéke (5 mA) éri el. Ezért a vételi ponton kell lennie egy érzékeny relének (erősítőnek), amelyet egy gyenge 5 mA-es impulzus kapcsol be, és az érintkezőjén keresztül egy másik, erősebb relét kapcsol be.

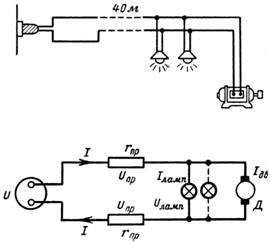
8. Milyen magas a lámpák feszültsége az ábra szerinti áramkörben? 28, ha: a) a motor nincs bekapcsolva; b) a motor beindul; c) a motor jár.

A motor és 20 db lámpa 110 V-os hálózatra csatlakozik A lámpák 110 V-ra és 40 W-ra vannak tervezve. A motor indítóárama Ip = 50 A, névleges árama In = 30 A.

A bevezetett rézhuzal keresztmetszete 16 mm2, hossza 40 m.

Ábra. A 7. ábrán és a probléma körülményei között látható, hogy a motor és a lámpa árama a hálózati feszültség csökkenését okozza, ezért a terhelési feszültség 110 V-nál kisebb lesz.

Rizs. 7.

U = 2 ∙ Ul + Ulamp.

Ezért a lámpákon lévő feszültség Ulamp = U-2 ∙ Ul.

Meg kell határozni a vezeték feszültségesését különböző áramoknál: Ul = I ∙ rl.

A teljes vonal ellenállása

2 ∙ rl = ρ ∙ (2 ∙ l) / S = 0,0178 ∙ (2 ∙ 40) / 16 = 0,089 Ohm.

Az összes lámpán áthaladó áram

20 ∙ Ilamp = 20 ∙ 40/110 = 7,27 A.

Hálózati feszültségesés, ha csak a lámpák világítanak (nincs motor),

2 ∙ Ul = Ilamp ∙ 2 ∙ rl = 7,27 ∙ 0,089 = 0,65 V.

A lámpák feszültsége ebben az esetben:

Ulamp = U-2 ∙ Ul = 110-0,65 = 109,35 V.

A motor indításakor a lámpák halványabban világítanak, mivel a vezetékben nagyobb a feszültségesés:

2 ∙ Ul = (Ilamp + Idv) ∙ 2 ∙ rl = (7,27 + 50) ∙ 0,089 = 57,27 ∙ 0,089 = 5,1 V.

A lámpák minimális feszültsége a motor indításakor:

Ulamp = Uc-2, Ul = 110-5,1 = 104,9 V.

Amikor a motor jár, a vezeték feszültségesése kisebb, mint a motor indításakor, de nagyobb, mint kikapcsolt motornál:

2 ∙ Ul = (Ilamp + Inom) ∙ 2 ∙ rl = (7,27 + 30) ∙ 0,089 = 37,27 ∙ 0,089 = 3,32 V.

A lámpák feszültsége a motor normál működése közben:

Ulamp = 110-3,32 = 106,68 V.

A lámpák feszültségének a névlegeshez viszonyított enyhe csökkenése is jelentősen befolyásolja a világítás fényerejét.