Az eredő ellenállás számítása soros-párhuzamos kapcsolásnál

Fogalmak és képletek

A soros-párhuzamos vagy vegyes kapcsolat három vagy több ellenállás összetett kapcsolata. A vegyes csatlakozás eredő ellenállását a soros és párhuzamos kötések ellenállásának kiszámítására szolgáló képletek segítségével szakaszosan számítják ki.

Példák

1. Számítsa ki három ellenállás soros-párhuzamos kapcsolatát az ábra diagramja alapján! 1.

Először cserélje ki a párhuzamosan kapcsolt r2 és r3 ellenállásokat a kapott r ellenállásra (2-3):

r (2-3) = (r2 ∙ r3) / (r2 + r3) = (10 ∙ 20) / 30 = 6,6 ohm.

A teljes áramkör eredő ellenállása r = r1 + r (2-3) = 5 + 6,6 = 11,6 ohm.

Rizs. 1.

2. Milyen áram folyik át az áramkörön (2. ábra) nyitott és zárt esetben késes kapcsoló P? Hogyan változik az r2 ellenálláson lévő feszültség mindkét esetben?

Rizs. 2.

a) A kapcsoló nyitva van. Sorosan kapcsolt r1 és r2 ellenállások eredő ellenállása

r (1-2) = r1 + r2 = 25 ohm.

Áram I (1-2) = U / r (1-2) = 100/25 = 4 A.

Feszültségesés az r2 ellenálláson

U2 = I (1-2) ∙ r2 = 4 ∙ 5 = 20 V.

b) A kapcsoló zárva van. A párhuzamosan kapcsolt r1 és r3 ellenállások eredő ellenállása

r (1-3) = (r1 ∙ r3) / (r1 + r3) = (20 ∙ 10) / (20 + 10) = 200/30 = 6,6 ohm.

A teljes áramkör teljes ellenállása r = r (1-3) + r2 = 6,6 + 5 = 11,6 ohm.

Áram I = U / r = 100 / 11,6 = 8,62 A.

A feszültségesés az r2 ellenálláson ebben az esetben egyenlő: U2 = I ∙ r2 = 8,62 ∙ 5 = 43,25 V.

A második esetben az áramerősség megnőtt az R3 párhuzamos ellenállás bekötése következtében. A több áram többet hoz létre feszültségesés ellenállásnál r2.

3. Mi legyen további ellenállás rd, hogy két párhuzamosan 120 V feszültségre és 0,2 A áramerősségre kapcsolt lámpa U = 220 V feszültségű hálózatba kapcsolható legyen (3. ábra)?

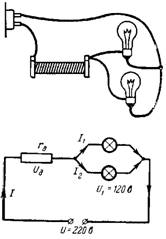
Rizs. 3.

A lámpákban lévő feszültségnek 120 V-nak kell lennie. A fennmaradó feszültség (100 V) az rd kiegészítő ellenállásra esik. Két I = 0,4 A lámpa árama folyik át az rd ellenálláson.

Ohm törvénye szerint rd = Ud / I = 100 / 0,4 = 250 Ohm.

4. Az 1,2 V-os izzószálú, 0,025 és 0,05 A izzószál árammal rendelkező elektronikus lámpák sorba vannak kötve egy 4,5 V-os egyenáramú feszültségforrással. Mennyi legyen a kiegészítő ellenállás rd ill. párhuzamos ellenállás (sönt) kisebb izzószáláramú lámpához (4. ábra)?

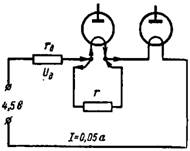
Rizs. 4.

Az áramkörben az ellenállásokat úgy kell megválasztani, hogy a második lámpa izzószálának árama I = 0,05 A. Az elektronikus lámpák izzószálának feszültsége 1,2 + 1,2 = 2,4 V. Ezt az értéket kivonva az akkumulátor feszültségéből, vegyük a feszültségesés értékét az rd kiegészítő ellenálláson: Ud = 4,5-2,4 = 2,1 V.

Ezért a járulékos ellenállás rd = (Ud) / I = 2,1 / 0,05 = 42 Ohm.

Az első vákuumcső izzószálán 0,05 A izzószál-áram nem haladhat át. Ennek az áramnak a felének (0,05-0,025 = 0,025 A) át kell haladnia az r söntön. A sönt feszültség megegyezik a lámpa izzószálával, azaz. 1,2 V. Ezért a sönt ellenállása: r = 1,2 / 0,025 = 48 Ohm.

5. Mekkora az eredő áramköri ellenállás és a benne lévő áram az ábra szerinti áramkörben? 5?

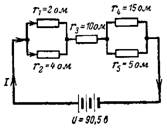
Rizs. 5.

Először is határozzuk meg a párhuzamosan kapcsolt ellenállások eredő ellenállását:

r (1-2) = (r1 ∙ r2) / (r1 + r2) = (2 ∙ 4) / (2 + 4) = 8/6 = 1,3 ohm;

r (4-5) = (r4 ∙ r5) / (r4 + r5) = (15 ∙ 5) / (15 + 5) = 75/20 = 3,75 ohm.

Az így kapott áramköri ellenállás:

r = r (1-2) + r3 + r (4-5) = 1,3 + 10 + 3,75 = 15,05 ohm.

A kapott áram U feszültségen = 90,5 V

I = U / r = 90,5 / 15,05 = 6 A.

6. Számítsa ki egy komplex soros-párhuzamos kapcsolat eredő ellenállását a 3. ábra áramkörében! 6. Számítsa ki az így kapott I áramot, I4 áramot és az r1 ellenálláson keresztüli feszültségesést!

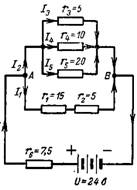
Rizs. 6.

Párhuzamosan kapcsolt ellenállások eredő vezetőképessége

1 / r (3-4-5) = 1 / r3 + 1 / r4 + 1 / r5 = 1/5 + 1/10 + 1/20 = 7/20 sim;

r (3-4-5) = 20/7 = 2,85 ohm.

Az r1 és r2 áramköri ellenállása:

r (1-2) = r1 + r2 = 15 + 5 = 20 ohm.

A kapott vezetőképesség és ellenállás az A és B pont között rendre egyenlő: 1 / rAB = 1 / r (3-4-5) + 1 / r (1-2) = 7/20 + 1/20 = 8/20 sim ; rAB = 20/8 = 2,5 ohm.

A teljes áramkör eredő ellenállása r = rAB + r6 = 2,5 + 7,5 = 10 ohm.

A kapott áramerősség I = U / r = 24/10 = 2,4 A.

Az A és B pontok közötti feszültség egyenlő az U forrásfeszültség mínusz az r6 ellenállás feszültségesése

UAB = U-I ∙ r6 = 24-(2,4 ∙ 7,5) = 6V.

Az r4 ellenállás ehhez a feszültséghez van kötve, így a rajta áthaladó áram egyenlő lesz:

I4 = UAB / r4 = 6/10 = 0,6A.

Az r1 és r2 ellenállások közös UAB feszültségeséssel rendelkeznek, így az r1-en áthaladó áram:

I1 = UAB / r (1-2) = 6/20 = 0,3 A.

Feszültségesés az r1 ellenálláson

Ur1 = I1 ∙ r1 = 0,3 ∙ 15 = 4,5 V.

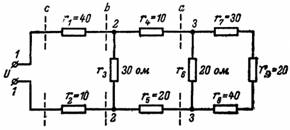
7. Mekkora az eredő ellenállás és áram az ábra szerinti áramkörben? 7 ha a forrásfeszültség U = 220 V?

Rizs. 7.

A 3. és 3. csomóponttól jobbra található áramkörrel kezdjük. Az r7, r8, r9 ellenállások sorba vannak kötve, ezért

r (7-8-9) = r7 + r8 + r9 = 30 + 40 + 20 = 90 ohm.

Ezzel az ellenállással párhuzamosan egy r6 ellenállás van kapcsolva, így a kapott ellenállás a 3. és 3. csomóponton (a szakasz)

ra = (r6 ∙ r (7-8-9)) / (r6 + r (7-8-9)) = (20 ∙ 90) / (20 + 90) = 1800/110 = 16,36 ohm.

Az r4 és r5 ellenállások sorba vannak kötve az ra ellenállással:

r (4-5-a) = 10 + 20 + 16,36 = 46,36 ohm.

A 2. és 2. csomópont eredő ellenállása (b szakasz)

rb = (r (4-5-a) ∙ r3) / (r (4-5-a) + r3) = (46,36 ∙ 30) / (46,36 + 30) = 1390,8 / 76, 36 = 18,28 ohm.

A teljes áramkör eredő ellenállása r = r1 + rb + r2 = 40 + 18,28 + 10 = 68,28 ohm.

A kapott áramerősség I = U / r = 220 / 68,28 = 3,8 A.