A kondenzátor kapacitásának kiszámítása

A C kapacitás a kondenzátor azon kapacitása, amely képes befogadni (tárolni és megtartani) a Q árammennyiséget ampermásodpercben vagy a Q töltést a függőben. Ha megmondunk egy testnek, például egy golyónak, egy elektromos töltést (az elektromosság mennyiségét) Q, akkor a test és a föld közé csatlakoztatott elektroszkóp U feszültséget fog mutatni (1. ábra). Ez a feszültség arányos a töltéssel, és függ a test alakjától és méretétől is.

A Q töltés és az U feszültség közötti összefüggést a Q = C ∙ U képlet fejezi ki.

A C arányossági állandót a test kapacitásának nevezzük. Ha a test golyó alakú, akkor a test kapacitása arányos a golyó r sugarával.

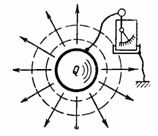
Rizs. 1.

A kapacitás mértékegysége a farad (F).

A test kapacitása 1 F, amikor 1 k töltés 1 V feszültséget hoz létre közte és a föld között. A faradok nagyon nagy mértékegységek, ezért a gyakorlatban kisebb mértékegységeket használnak: mikrofarad (μF), nanofarad (nF) és picofarad (pF)...

Ezeket az egységeket a következő arányok kapcsolják össze: 1 Ф = 10 ^ 6 μF; 1 μF = 10 ^ 6 pF; 1 nF = 10^3 pF.

Egy 1 cm sugarú golyó kapacitása 1,1 pF.

Nemcsak egy izolált test képes töltést felhalmozni, hanem egy speciális eszköz, az úgynevezett kondenzátor is. A kondenzátor két vagy több lemezből (lemezből) áll, amelyeket dielektrikum (szigetelés) választ el egymástól.

ábrán. A 2. ábra egy kondenzátorhoz csatlakoztatott egyenáramú áramkört mutat. Bekapcsoláskor a kondenzátor jobb oldali lapjában pozitív töltés +Q, a bal oldali lemezben pedig negatív –Q töltés jön létre. Alatt kondenzátor töltés áram folyik át az áramkörön, amely a töltés befejezése után leáll; akkor a kondenzátoron lévő feszültség egyenlő lesz e-vel. stb. c) forrás U. A kondenzátorlap töltése, a feszültség és a kapacitás a Q = C ∙ U aránnyal függ össze. Ebben az esetben a kondenzátor dielektrikumában elektrosztatikus tér jön létre.

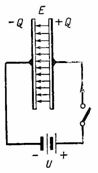
Rizs. 2.

A légdielektrikummal rendelkező kondenzátor kapacitása a következő képlettel számítható ki: C = S / (4 ∙ π ∙ d) ∙ 1,11, pF, ahol S egy lemez területe, cm2; d a lemezek közötti távolság, cm; C a kondenzátor kapacitása, pF.

Egy n lemezből álló kondenzátor kapacitása (3. ábra) egyenlő: C = (n-1) ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.

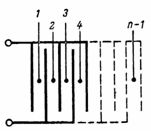
Rizs. 3.

Ha a lemezek közötti teret más dielektrikummal, például papírral töltjük ki, a kondenzátor kapacitása ε-szeresére nő. Papírszigeteléssel a kapacitás háromszorosára nő, csillámszigeteléssel 5-8-szorosra, üveggel 7-szeresére stb. ε értékét a dielektrikum dielektromos állandójának nevezzük.

Az ε (epsilon) dielektromos állandójú kondenzátor kapacitásának meghatározására szolgáló általános képlet: C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.

Ez a képlet hasznos a rádiók kis változó kondenzátorainak kiszámításához.Ugyanez a képlet a következőképpen ábrázolható: C = (ε_0 ∙ ε ∙ S) / d, ahol ε_0 a vákuum dielektromos állandója vagy dielektromos állandója (ε_0 = 8,859 ∙ 10 ^ (- 12) F / m); ε a dielektrikum dielektromos állandója.

Ebben a képletben a méreteket méterben helyettesítjük, a kapacitást pedig faradban kapjuk meg.

Példák

1. Mekkora a Föld bolygó kapacitása, amelynek sugara r = 6378 km?

Mivel egy 1 cm sugarú gömb kapacitása 1,11 pF, a Föld kapacitása: C = 637,8 ∙ 10 ^ 6 ∙ 1,11 = 707,95 ∙ 10 ^ 6 pF = 708 μ. (Egy bolygónk méretű golyó kapacitása viszonylag kicsi. A kis méretű elektrolitkondenzátorok rendelkeznek ezzel a kapacitással).

2. Határozza meg egy két lemezből álló kondenzátor kapacitását, amelyek mindegyikének területe S = 120 cm2!

A lemezeket légréteg választja el egymástól, amelynek vastagsága d = 0,5 cm, C = S / (4 ∙ π ∙ d) ∙ 1,11 = (120 ∙ 1,11) / (4 ∙ π ∙ 0,5) = 21 ,20 pF ...

3. Határozza meg a kondenzátor kapacitását az előző példában megadott adatokkal, ha a lemezek közötti teret ε = 4 dielektromos állandójú viaszpapírral, üveggel (ε = 7), elektromos kartonnal (ε = 2) töltjük ki! , csillám (ε = 8).

Egy viaszpapír kondenzátor kapacitása C = ε ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = 4 ∙ 21,2 = 84,8 pF.

Az üvegkondenzátor kapacitása C = 7 ∙ 21,2 = 148,4 pF.

A karton kondenzátor kapacitása C = 2 ∙ 21,2 = 42,3 pF.

A csillámkondenzátor kapacitása C = 8 ∙ 21,2 = 169,6 pF.

4. Mekkora a levegős forgókondenzátor kapacitása egy 20 db 20 cm2-es lemezből álló rádióvevőhöz, ha a lemezek közötti távolság 0,06 cm (149. ábra)?

C = (n-1) ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = (20-1) ∙ (20 ∙ 1,11) / (4 ∙ π ∙ 0,06) = 559, 44 pF.

ábrán látható kondenzátor.A 3. ábra különálló legegyszerűbb, két lemezes kondenzátorokból áll, amelyek száma n-1.

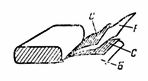
5. A C = 2 μF kapacitású papírkondenzátor két C ónfólia csíkból és két ε = 6 dielektromos állandójú B viaszpapírból készült dielektrikumból áll. A viaszpapír vastagsága d = 0,1 mm. Az összehajtott szalagokat feltekerjük, a vezetékeket az acéllemezekből készítjük. Határozza meg a kondenzátor acélszalag hosszát, ha szélessége 4 cm (4. ábra).

Rizs. 4.

Először egy csík területét a következő képlettel határozzuk meg: C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1,11, ahonnan S = (C ∙ 4 ∙ π ∙ d) / (ε ∙ 1,11) = ( 2 ∙ 4 ∙ π ∙ 0,01 ∙ 10 ^ 6) / (6 ∙ 1,11); S = 2 000 000 / (6 ∙ 1,11) ∙ 4 ∙ π ∙ 0,01 = 37680 cm2.

Az egyes csíkok hossza l = 37680/4 = 9420 cm = 94,2 m.