Az elektromágnesek vonóereje
 Az az erő, amellyel az elektromágnes vonzza a ferromágneses anyagokat, az F mágneses fluxustól vagy ennek megfelelően a B indukciótól és az S elektromágnes keresztmetszeti területétől függ.
Az az erő, amellyel az elektromágnes vonzza a ferromágneses anyagokat, az F mágneses fluxustól vagy ennek megfelelően a B indukciótól és az S elektromágnes keresztmetszeti területétől függ.
Az elektromágnes nyomóerejét a képlet határozza meg
F = 40550 ∙ B ^ 2 ∙ S,
ahol F az elektromágnes nyomóereje, kg (az erőt newtonban is mérjük, 1 kg = 9,81 N vagy 1 N = 0,102 kg); B – indukció, T; S az elektromágnes keresztmetszete, m2.
Példák
1. A csaptelep elektromágnese egy mágneses áramkör (1. ábra). Mekkora a patkódaru elektromágnes emelőereje, ha a mágneses indukció B = 1 T, és az elektromágnes minden pólusának keresztmetszete S = 0,02 m2 (1. ábra, b)? Figyelmen kívül hagyja az elektromágnes és az armatúra közötti rés hatását.
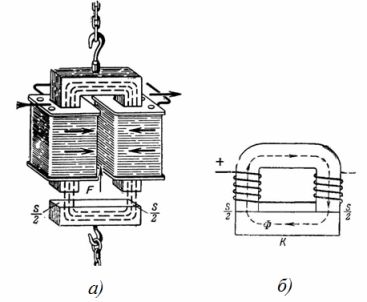
Rizs. 1. Emelő elektromágnes
F = 40550 ∙ B ^ 2 ∙ S; F = 40550 ∙ 1 ^ 2 ∙ 2 ∙ 0,02 = 1622 kg.
2. Egy kör alakú acél elektromágnes az ábrán látható méretekkel rendelkezik. 2, a és b. Az elektromágnes emelőereje 3 T. Határozza meg az elektromágnes mag keresztmetszeti területét, n. p. és a tekercs menetszáma I = 0,5 A mágnesező áram mellett.
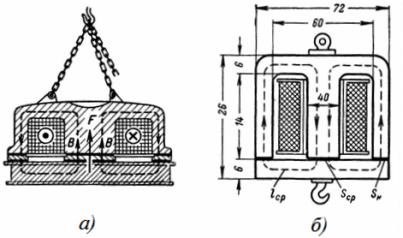
Rizs. 2. Kerek elektromágnes
A mágneses fluxus áthalad a kör alakú belső magon, és visszatér a hengeres testen. Az Sc mag és a ház Sk keresztmetszete megközelítőleg azonos, ezért az indukciós értékek a magban és a burkolatban gyakorlatilag megegyeznek:
Sc = (π ∙ 40 ^ 2) / 4 = (3,14 ∙ 1600) / 4 = 1256 cm2 = 0,1256 m2,
Sk = ((72 ^ 2-60 ^ 2) ∙ π) / 4 = 3,14 / 4 ∙ (5184-3600) = 1243,5 cm2 = 0,12435 m2;
S = Sc + Sk = 0,24995 m2 ≈0,25 m2.
Az elektromágnesben szükséges indukciót az F = 40550 ∙ B ^ 2 ∙ S képlet határozza meg,
ahol B = √ (F / (40550 ∙ S)) = √ (3000 / (40550 ∙ 0,25)) = 0,5475 T.
A feszültség ennél az indukciónál az öntött acél mágnesezési görbéjén található:
H = 180 A/m.
A mezővonal átlagos hossza (2. ábra, b) lav = 2 ∙ (20 + 23) = 86 cm = 0,86 m.
Mágnesesítő erő I ∙ ω = H ∙ lav = 180 ∙ 0,86 = 154,8 Av; I = (I ∙ ω) / I = 154,8 / 0,5 = 310 A.
Valójában n. s, vagyis az áramerősségnek és a fordulatok számának sokszorosának kell lennie, mivel az elektromágnes és az armatúra között elkerülhetetlen légrés keletkezik, ami jelentősen megnöveli a mágneses áramkör mágneses ellenállását. Ezért az elektromágnesek kiszámításakor figyelembe kell venni a légrést.
3. A csaptelep elektromágnesének tekercse 1350 fordulatú, I = 12 A áram folyik át rajta. 3. Mekkora súlyt emel fel az elektromágnes az armatúrától 1 cm távolságra, és milyen súlyt bír el a gravitáció után?

Rizs. 3. Elektromágneses tekercs
Az I ∙ ω értékkel rendelkező N. nagy részét a légrésen keresztüli mágneses fluxus vezetésére fordítják: I ∙ ω≈Hδ ∙ 2 ∙ δ.
Mágnesesítő erő I ∙ ω = 12 ∙ 1350 = 16200 A.
Mivel H ∙ δ = 8 ∙ 10 ^ 5 ∙ B, akkor Hδ ∙ 2 ∙ δ = 8 ∙ 10 ^ 5 ∙ B ∙ 0,02.
Ezért 16200 = 8 ∙ 10 ^ 5 ∙ B ∙ 0,02, azaz. B = 1,012 T.
Feltételezzük, hogy az indukció B = 1 T, mivel n része. c) I ∙ ω-t mágneses fluxus vezetésére fordítják acélban.
Ellenőrizzük ezt a számítást az I ∙ ω = Hδ ∙ 2 ∙ δ + Hс ∙ lс képlettel.
A mágneses vonal átlagos hossza: lav = 2 ∙ (7 + 15) = 44 cm = 0,44 m.
A Hc intenzitást B = 1 T (10000 Gs) mellett a mágnesezési görbe alapján határozzuk meg:
Hc = 260 A/m. I ∙ ω = 0,8 ∙ B ∙ 2 + 2,6 ∙ 44 = 1,6 ∙ 10000 + 114,4 = 16114 Át.
A B = 1 T indukciót létrehozó mágnesező erő I ∙ ω = 16114 Av gyakorlatilag megegyezik az adott n-nel. v. I ∙ ω = 16200 Át.
A mag és a kúp teljes keresztmetszete: S = 6 ∙ 5 + 2 ∙ 5 ∙ 3 = 0,006 m2.
Az elektromágnes F = 40550 ∙ B ^ 2 ∙ S = 40550 ∙ 1 ^ 2 ∙ 0,006 = 243,3 kg súlyú töltést vonz magához 1 cm távolságból.
Mivel az armatúra felhúzása után a légrés gyakorlatilag megszűnik, az elektromágnes sokkal nagyobb terhelést is elbír. Ebben az esetben az egész n. c) I ∙ ω-t csak acélban használjuk mágneses fluxus vezetésére, ezért I ∙ ω = Hс ∙ lс; 16200 = Hs ∙ 44; Hc = 16200/44 = 368 A/cm = 36800 A/m.
Ilyen feszültség mellett az acél gyakorlatilag telített, és az indukció benne kb. 2 T. Az elektromágnes F = 40550 ∙ B ^ 2 ∙ S = 40550 ∙ 4 ∙ 0,006 = 973 kg erővel vonzza az armatúrát.
4. A jel (villogó) relé egy páncélozott 1 körmagú elektromágnesből és egy 2 szelep típusú armatúrából áll, amely az elektromágnes áramellátása után magához vonzza és elengedi a 3 villogót, amely megnyitja a jel számjegyét (ábra). 4).
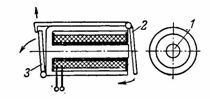
Rizs. 4. Páncél elektromágnes
A mágnesezési szilárdság I ∙ ω = 120 Av, a légrés δ = 0,1 cm, az elektromágnes teljes keresztmetszete S = 2 cm2. Becsülje meg a relé húzóerejét.
A B induktivitást egymást követő közelítésekkel határozzuk meg az I ∙ ω = Hс ∙ lс + Hδ ∙ 2 ∙ δ egyenlet felhasználásával.
Legyen n. c) Hc ∙ lc 15% I ∙ ω, azaz. 18 Av.
Ekkor I ∙ ω-Hс ∙ lс = Hδ ∙ 2 ∙ δ; 120-18 = Hδ ∙ 0,2; Hδ = 102/0,2 = 510 A/cm = 51000 A/m.
Ezért találjuk a B indukciót:
Hδ = 8 ∙ 10 ^ 5 V; B = Hδ / (8 ∙ 10 ^ 5) = 51 000 / (8 ∙ 10 ^ 5) = 0,0637 T.
Miután behelyettesítettük a B értéket az F = 40550 ∙ B ^ 2 ∙ S képletben, a következőt kapjuk:
F = 40550 ∙ 0,0637 ^ 2 ∙ 0,0002 = 0,0326 kg.
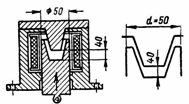
5. Az egyenáramú fék mágnesszelepének (5. ábra) kúpos ütközővel ellátott dugattyús armatúrája van. Az armatúra és a mag távolsága 4 cm A munkaátmérő (kör alakú érintkezési felületű magok) d = 50 mm. Az armatúrát 50 kg-os erővel a tekercsbe húzzuk. A középső erővonal hossza lav = 40 cm. Határozzuk meg n. pp. és a tekercsáram, ha 3000 fordulat van.
Rizs. 5. DC fék mágnesszelep
Az elektromágnes munkarészének területe megegyezik egy d = 5 cm átmérőjű kör területével:
S = (π ∙ d ^ 2) / 4 = 3,14 / 4 ∙ 25 = 19,6 cm2.
Az F = 50 kg erő létrehozásához szükséges B indukció az F = 40550 ∙ B ^ 2 ∙ S egyenletből adódik,
ahol B = √ (F / (40550 ∙ S)) = √ (50 / (40550 ∙ 0,00196)) = 0,795 T.
Mágnesesítő erő I ∙ ω = Hс ∙ lс + Hδ ∙ δ.
A Hc ∙ lc acél mágnesezési szilárdságát egyszerűsített módon határozzuk meg, abból a tényből kiindulva, hogy ez 15% I ∙ ω:
I ∙ ω = 0,15 ∙ I ∙ ω + Hδ ∙ δ; 0,85 ∙ I ∙ ω = Hδ ∙ δ; 0,85 ∙ I ∙ ω = 8 ∙ 10 ^ 5 ∙ B ∙ δ; I ∙ ω = (8 ∙ 10 ^ 5 ∙ 0,795 ∙ 0,04) / 0,85 = 30 000 Át.
Mágnesező áram I = (I ∙ ω) / ω = 30000/3000 = 10 A.