Mágneses térerősség. Mágnesesítő erő
 A vezeték vagy tekercs körül mindig van elektromos áram mágneses mező… Az állandó mágnes mágneses terét az elektronok mozgása okozza a pályájukon az atomban.
A vezeték vagy tekercs körül mindig van elektromos áram mágneses mező… Az állandó mágnes mágneses terét az elektronok mozgása okozza a pályájukon az atomban.
A mágneses mezőt az erőssége jellemzi. A mágneses tér H erőssége hasonló a mechanikai szilárdsághoz. Ez egy vektormennyiség, vagyis van nagysága és iránya.
A mágneses teret, vagyis a mágnes körüli teret úgy ábrázolhatjuk, hogy mágneses vonalak töltik ki, amelyek a mágnes északi pólusából kilépnek és a déli pólusba lépnek (1. ábra). A mágneses vonal érintői a mágneses térerősség irányát jelzik.
A mágneses tér erősebb ott, ahol a mágneses vonalak sűrűbbek (a mágnes pólusainál vagy egy áramvezető tekercs belsejében).
Minél nagyobb az I áram és a tekercs ω fordulatszáma, annál nagyobb a mágneses tér a vezeték közelében (vagy a tekercsen belül).
A H mágneses tér erőssége a tér bármely pontjában annál nagyobb, minél nagyobb a ∙ ω szorzat és minél rövidebb a mágneses vonal hossza:
H = (I ∙ ω) / l.
Az egyenletből következik, hogy a mágneses tér erősségének mérési egysége az amper méterenként (A / m).
Egy adott egyenletes térben minden mágneses vonalra a H1 ∙ l1 = H2 ∙ l2 = … = H ∙ l = I ∙ ω szorzat egyenlő (1. ábra).
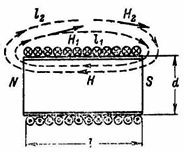
Rizs. 1.
A mágneses áramkörökben a H ∙ l szorzat hasonló az elektromos áramkörök feszültségéhez, mágneses feszültségnek nevezzük, a mágneses indukciós vonal teljes hosszában pedig mágnesező erőnek (ns) nevezzük Fm: Fm = H ∙ l = I ∙ ω.
Az Fm mágnesező erő mérése amperben történik, de a műszaki gyakorlatban az amper elnevezés helyett az amper-turn elnevezést használják, ami hangsúlyozza, hogy Fm arányos az áramerősséggel és a fordulatok számával.
Egy mag nélküli hengeres tekercsnél, amelynek hossza jóval nagyobb, mint az átmérője (l≫d), a tekercsen belüli mágneses tér egységesnek tekinthető, azaz. azonos H mágneses térerővel a tekercs teljes belső terében (1. ábra). Mivel a mágneses tér egy ilyen tekercsen kívül sokkal gyengébb, mint a belsejében, a külső mágneses tér elhanyagolható, és a számításnál azt feltételezzük, hogy n. c tekercs egyenlő a tekercsen belüli térerősség szorzata a tekercs hosszával.
A vezeték és az áramtekercs mágneses terének polaritását a kardánszabály határozza meg. Ha a gimbal előre mozgása egybeesik az áram irányával, akkor a kardánkar forgásiránya jelzi a mágneses vonalak irányát.
Példák
1. Egy 2000 fordulatú tekercsen 3 A áram folyik át. Mi az n. v. tekercsek?
Fm = I ∙ ω = 3 ∙ 2000 = 6000 A. A tekercs mágnesezési erőssége 6000 amper-fordulat.
2. Egy 2500 fordulatú tekercsnek n-nek kell lennie. o. 10000 A. Milyen áramnak kell átfolynia rajta?
I = Fm / ω = (I ∙ ω) / ω = 10000/2500 = 4 A.
3.A tekercsen I = 2 A áram folyik át. Hány fordulatnak kell lennie a tekercsben, hogy n legyen. falu 8000 A?
ω = Fm / I = (I ∙ ω) / I = 8000/2 = 4000 fordulat.
4. Egy 10 cm hosszú, 100 fordulattal rendelkező tekercs belsejében biztosítani kell a H = 4000 A / m mágneses tér erősségét. Mekkora áramot kell vinnie a tekercsnek?
A tekercs mágnesező ereje Fm = H ∙ l = I ∙ ω. Ezért 4000 A / m ∙ 0,1 m = I ∙ 100; I = 400/100 = 4 A.
5. A tekercs (szolenoid) átmérője D = 20 mm, hossza l = 10 cm A tekercs d = 0,4 mm átmérőjű rézhuzalból van feltekercselve. Mekkora a mágneses térerősség a tekercsen belül, ha 4,5 V-on van bekapcsolva?
A fordulatok száma a szigetelés vastagságának figyelembevétele nélkül ω = l∶d = 100∶0,4 = 250 fordulat.
A hurok hossza π ∙ d = 3,14 ∙ 0,02 m = 0,0628 m.
A tekercs hossza l1 = 250 ∙ 0,0628 m = 15,7 m.
A tekercs aktív ellenállása r = ρ ∙ l1 / S = 0,0175 ∙ (4 ∙ 15,7) / (3,14 ∙ 0,16) = 2,2 Ohm.
Áram I = U / r = 4,5 / 2,2 = 2,045 A ≈2 A.
A mágneses tér erőssége a tekercsen belül H = (I ∙ ω) / l = (2 ∙ 250) / 0,1 = 5000 A / m.
6. Határozza meg a mágneses tér erősségét 1, 2, 5 cm távolságra attól az egyenes vezetéktől, amelyen keresztül az I = 100 A áram folyik!
Használjuk a H ∙ l = I ∙ ω képletet.
Egyenes vezeték esetén ω = 1 és l = 2 ∙ π ∙ r,
ahol H = I / (2 ∙ π ∙ r).
H1 = 100 / (2 ∙ 3,14 ∙ 0,01) = 1590 A/m; H2 = 795 A/m; H3 = 318 A/m.

