Lineáris és pontszerű fényforrások

Méret szerint a világ összes forrása feltételesen két csoportra osztható:

• pont,

• lineáris.

Pontszerű fényforrásnak nevezzük azt a fényforrást, amelynek méretei a sugárvevő távolságához képest olyan kicsik, hogy elhanyagolhatóak.

A gyakorlatban pontszerű fényforrásnak azt tekintjük, amelynek legnagyobb L mérete legalább 10-szer kisebb, mint a sugárzásvevő r távolsága (1. ábra).

Az ilyen sugárforrások esetében a megvilágítást az E = (I / r2)·cosα képlet határozza meg,

ahol E, I – a sugárforrás felületi megvilágítása és fényintenzitása; r a fényforrás és a fotodetektor távolsága; α – az a szög, amellyel a fotodetektor eltolódott a normáltól.

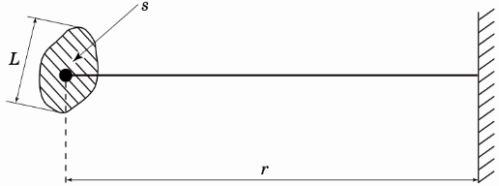
Rizs. 1. Pontos fényforrás

Például, ha egy 10 cm átmérőjű lámpa 100 m távolságból megvilágít egy felületet, akkor ez a lámpa pontforrásnak tekinthető. De ha ugyanannak a lámpának a távolsága a felülettől 50 cm, akkor a lámpa már nem tekinthető pontforrásnak.A pontszerű fényforrás tipikus példája egy csillag az égen. A csillagok mérete óriási, de a távolságuk a Földtől sok nagyságrenddel nagyobb.

A beépített világítótestekhez való halogén és LED lámpák pontszerű fényforrásnak minősülnek az elektromos világításban. A LED gyakorlatilag pontszerű fényforrás, mert kristálya mikroszkopikus méretű.

A lineáris sugárforrások közé tartoznak azok az sugárzók, amelyek relatív méretei minden irányban nagyobbak, mint egy pontsugárzó méretei. A megvilágítási mérési síktól való távolság növekedésével egy ilyen sugárzó relatív méretei elérhetik azt az értéket, hogy ez a sugárforrás pontforrássá válik.

Példák elektromos lineáris fényforrásokra: fénycsövek, lineáris LED lámpák, LED RGB-szalagokkal. De értelemszerűen minden olyan forrás, amely nem tekinthető pontforrásnak, lineáris (kiterjesztett) fényforrásnak tulajdonítható.

Ha onnan, ahol egy pontszerű sugárforrás található, a fényintenzitásvektorokat a térben különböző irányokba választjuk el, és a végeiken keresztül felületet rajzolunk, akkor megkapjuk a sugárforrás fotometriai testét. Egy ilyen test teljes mértékben jellemzi a sugárzási fluxus térbeli eloszlását.

A fényintenzitás térbeli eloszlásának jellege szerint a pontforrásokat is két csoportra osztják. Az első csoportba azok a források tartoznak, amelyeknek a fényintenzitása egy adott tengelyhez képest szimmetrikus eloszlású (2. ábra). Az ilyen forrást körszimmetrikusnak nevezzük.

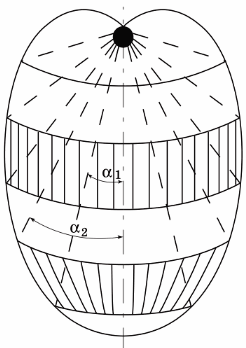
Rizs. 2.Szimmetrikus radiátor modellje

Ha a forrás körszimmetrikus, akkor a fotometriai teste egy forgástest, és teljes mértékben jellemezhető a forgástengelyen átmenő függőleges és vízszintes metszetekkel (3. ábra).

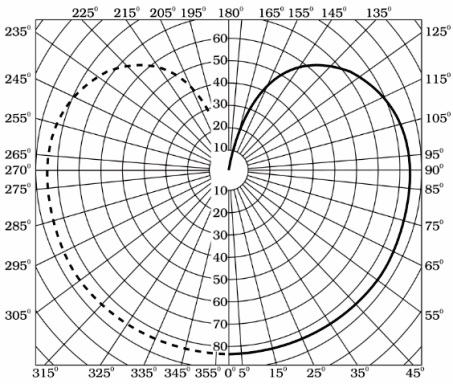
Rizs. 3. Szimmetrikus fényforrás fényintenzitás-eloszlásának hosszanti görbéje

A második csoport aszimmetrikus fényintenzitás-eloszlású forrásokból áll. Aszimmetrikus forrásban a fényintenzitás-elosztó testnek nincs szimmetriatengelye. Egy ilyen forrás jellemzésére hosszirányú fényintenzitási görbék családját szerkesztjük, amelyek megfelelnek a tér különböző irányainak, például 30 ° után, amint az 1. ábrán látható. 4. Általában az ilyen grafikonokat poláris koordinátákkal ábrázolják.

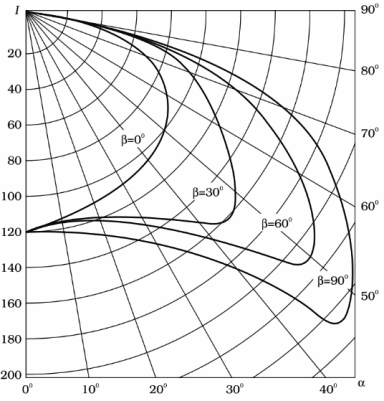
Rizs. 4. Kiegyensúlyozatlan fényforrás fényintenzitás-eloszlásának longitudinális görbéi