Veszteségek és feszültségesések - mi a különbség?

A hétköznapi emberi életben a "vesztés" és a "bukás" szavakat bizonyos teljesítmények csökkenésének tényére használják, de ezek más értéket jelentenek.

Ebben az esetben a „veszteségek” egy alkatrész elvesztését, sérülését, a korábban elért szint méretének csökkentését jelentik. A veszteségek nem kívánatosak, de elviselheti őket.

A „zuhanás” szó alatt komolyabb sérelem értendő, amely a jogok teljes megfosztásával jár együtt. Így még az időnként előforduló veszteségek (mondjuk egy portfólió) is visszaeséshez vezethetnek (például az anyagi élettartam szintje).

Ebben a tekintetben ezt a kérdést az elektromos hálózat feszültségével kapcsolatban vizsgáljuk meg.

Hogyan keletkeznek a veszteségek és a feszültségesések

A villamos energiát nagy távolságokra a felsővezetékek szállítják egyik alállomásról a másikra.

A felsővezetékeket a megengedett teljesítmény továbbítására tervezték, és bizonyos anyagú és szakaszú fémhuzalokból készülnek. Rezisztív terhelést hoznak létre, amelynek ellenállásértéke R és reaktív terhelése X.

A fogadó oldalon áll transzformátorvillamos energia átalakítás.Tekercsei aktív és kifejezett XL induktív ellenállással rendelkeznek. A transzformátor szekunder oldala lecsökkenti a feszültséget és továbbítja a fogyasztókhoz, akiknek a terhelése Z értékkel fejeződik ki, és természetében aktív, kapacitív és induktív. Ez befolyásolja a hálózat elektromos paramétereit is.

A légvezeték tartójának vezetékeire, az erőátviteli alállomáshoz legközelebb eső feszültség minden fázisban legyőzi az áramkör reaktív és aktív ellenállását, és áramot hoz létre benne, amelynek vektora eltér az áramkör vektorától. φ szöggel alkalmazott feszültség.

A feszültségek eloszlásának és az áramok áramlásának jellege a vonal mentén szimmetrikus terhelési mód esetén a képen látható.

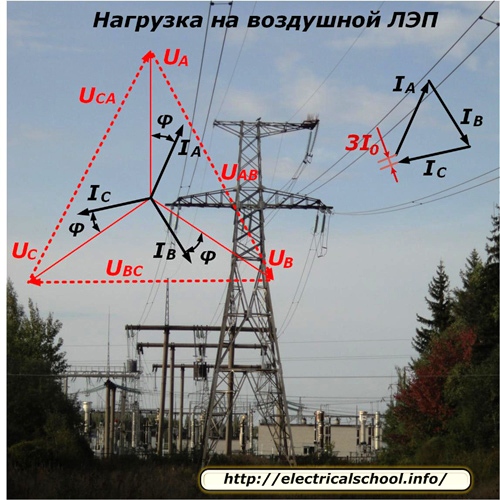
Mivel a vezeték minden fázisa különböző számú fogyasztót táplál, akik szintén véletlenszerűen kapcsolódnak le vagy kapcsolódnak be a munkába, technikailag nagyon nehéz a fázisterhelést tökéletesen kiegyenlíteni. Mindig van benne kiegyensúlyozatlanság, amit a fázisáramok vektoros összeadása határoz meg és 3I0-nak ír fel. A legtöbb számításnál egyszerűen figyelmen kívül hagyják.

Az adó alállomás által fogyasztott energia részben a vezeték ellenállásának leküzdésére fordítódik, és kis változtatással jut el a vevőoldalra. Ezt a törtrészt veszteség és feszültségesés jellemzi, amelynek vektora amplitúdója kissé csökken, és minden fázisban egy szöggel eltolódik.

A veszteségek és a feszültségesés kiszámítása

A villamos energia átvitele során lejátszódó folyamatok megértéséhez a vektoros forma alkalmas a fő jellemzők ábrázolására. Különféle matematikai számítási módszerek is ezen a módszeren alapulnak.

A számítások egyszerűsítése érdekében háromfázisú rendszer három egyfázisú egyenértékű áramkör képviseli. Ez a módszer jól működik szimmetrikus terhelés esetén, és lehetővé teszi a folyamatok elemzését, amikor megszakad.

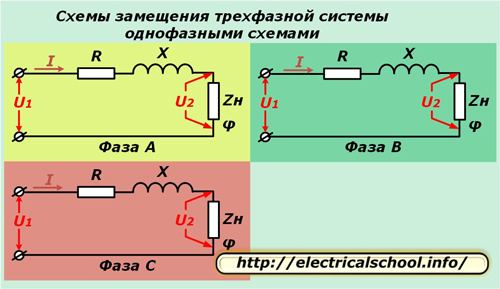
A fenti ábrákon a vezeték minden egyes vezetőjének aktív R és X reaktanciája sorba van kötve a φ szöggel jellemzett Zn komplex terhelési ellenállással.

Ezenkívül egy fázisban kiszámítják a feszültségveszteséget és a feszültségesést. Ehhez meg kell adni az adatokat. Erre a célra egy energiát fogadó alállomást választanak ki, ahol már meg kell határozni a megengedett terhelést.

Bármely nagyfeszültségű rendszer feszültségértéke már szerepel a referenciakönyvekben, a vezetékek ellenállását pedig azok hossza, keresztmetszete, anyaga és a hálózat konfigurációja határozza meg. Az áramkör maximális áramát a vezetékek tulajdonságai határozzák meg és korlátozzák.

Ezért a számítások megkezdéséhez a következőkre van szükségünk: U2, R, X, Z, I, φ.

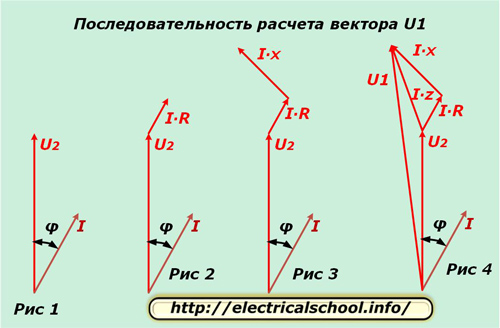
Vegyünk egy fázist, például «A»-t, és a komplex síkban elválasztjuk az U2 és I vektorokat, amelyek φ szöggel el vannak tolva, amint az 1. ábrán látható. A vezető aktív ellenállásának potenciálkülönbsége irányban egybeesik Az áramerősséget és a nagyságát az I ∙ R kifejezés határozza meg. Ezt a vektort elhalasztjuk az U2 végétől (2. ábra).

A vezető reaktanciájának potenciálkülönbsége φ1 szöggel tér el az áram irányától, és az I ∙ X szorzatból számítjuk ki. Elhalasztjuk az I ∙ R vektorból (3. ábra).

Emlékeztető: a vektorok pozitív forgásiránya esetén a komplex síkban az óramutató járásával ellentétes mozgást veszik. Az induktív terhelésen átfolyó áram szöggel lemarad az alkalmazott feszültségtől.

A 4. ábra a potenciálkülönbség vektorok ábrázolását mutatja az I ∙ Z teljes vezetékellenálláson és az U1 áramkör bemeneti feszültségén.

Most összehasonlíthatja a bemeneti vektorokat az egyenértékű áramkörrel és a terhelésen keresztül. Ehhez helyezze vízszintesen a kapott diagramot (5. ábra), és rajzoljon egy ívet az elejétől az U1 modul sugarával, amíg az nem metszi az U2 vektor irányát (6. ábra).

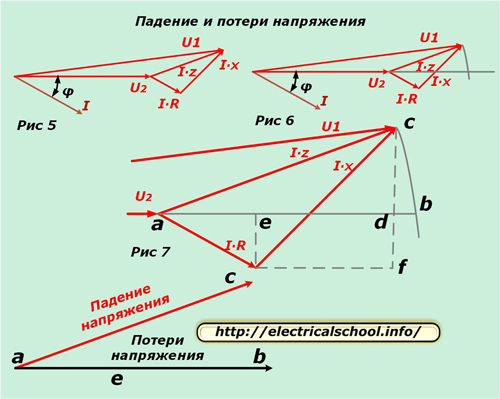
A 7. ábra a háromszög nagyítását mutatja a jobb áttekinthetőség érdekében, valamint a segédvonalak megrajzolását, amelyek a karakterisztikus metszéspontokat jelzik betűkkel.

A kép alján látható, hogy a kapott ac vektort feszültségesésnek, az ab-t veszteségnek nevezzük. Méretben és irányban különböznek egymástól. Ha visszatérünk az eredeti skálához, látni fogjuk, hogy az ac-t a vektorok geometriai kivonásával kapjuk (U2 az U1-ből), ab pedig aritmetikai. Ez a folyamat az alábbi képen látható (8. ábra).

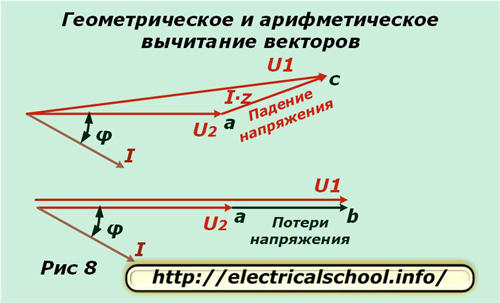
Feszültségveszteség számítási képletek levezetése

Most térjünk vissza a 7. ábrához, és vegyük észre, hogy a bd szegmens nagyon kicsi. Emiatt a számítások során figyelmen kívül hagyjuk, és a feszültségveszteséget a szegmenshossz ad-ból számítjuk. Két ae és ed vonalszakaszból áll.

Mivel ae = I ∙ R ∙ cosφ és ed = I ∙ x ∙ sinφ, akkor egy fázis feszültségvesztesége a következő képlettel számítható ki:

∆Uph = I ∙ R ∙ cosφ + I ∙ x ∙ sinφ

Ha feltételezzük, hogy a terhelés minden fázisban szimmetrikus (feltételesen figyelmen kívül hagyva a 3I0-t), akkor matematikai módszerekkel számíthatjuk ki a vezeték feszültségveszteségét.

∆Ul = √3I ∙ (R ∙ cosφ + x ∙ sinφ)

Ha ennek a képletnek a jobb oldalát megszorozzuk és elosztjuk az Un hálózati feszültséggel, akkor egy olyan képletet kapunk, amely lehetővé teszi a tápegységen keresztüli feszültségveszteségek p kiszámítását.

∆Ul = (P ∙ r + Q ∙ x) / Un

Az aktív P és a meddő Q teljesítmény értékeit a vezetékmérők leolvasásából lehet venni.

Így az elektromos áramkör feszültségvesztesége a következőktől függ:

• az áramkör aktív és reaktanciája;

• az alkalmazott teljesítmény összetevői;

• az alkalmazott feszültség nagysága.

A feszültségesés keresztirányú komponensének számítására szolgáló képletek levezetése

Térjünk vissza a 7. ábrához. Az ac vektor értékét egy acd derékszögű háromszög hipotenuzusával ábrázolhatjuk. A hirdetés lábát már kiszámoltuk. Határozzuk meg a cd keresztirányú komponenst.

Az ábrán látható, hogy cd = cf-df.

df = ce = I ∙ R ∙ sin φ.

cf = I ∙ x ∙ cos φ.

cd = I ∙ x ∙ cosφ-I ∙ R ∙ sinφ.

A kapott modellek segítségével kis matematikai transzformációkat végzünk, és megkapjuk a feszültségesés keresztirányú komponensét.

δU = √3I ∙ (x ∙ cosφ-r ∙ sinφ) = (P ∙ x-Q ∙ r) / Un.

Az U1 feszültség kiszámítására szolgáló képlet meghatározása a tápvezeték elején

Ismerve az U2 vonal végén lévő feszültség értékét, a ∆Ul veszteséget és a δU esés keresztirányú komponensét, a Pitagorasz-tétel segítségével kiszámíthatjuk az U1 vektor értékét. Kibővített formában a következő formája van.

U1 = √ [(U2 + (Pr + Qx) / Un)2+ ((Px-Qr) / Un)2].

Gyakorlati használat

A feszültségveszteségek kiszámítását mérnökök végzik az elektromos áramköri projekt létrehozásának szakaszában a hálózat és annak alkotóelemeinek optimális kiválasztásához.

Az elektromos berendezések üzemeltetése során szükség esetén a vezetékek végén a feszültségvektorok egyidejű mérése időszakonként elvégezhető, és az egyszerű számítások módszerével kapott eredmények összehasonlíthatóak. követelményeknek a nagy munkapontosság szükségessége miatt.

Feszültségveszteségek a szekunder körökben

Példa erre a feszültségmérő transzformátorok szekunder áramkörei, amelyek időnként több száz métert is elérnek, és speciális, megnövelt keresztmetszetű tápkábellel továbbítják.

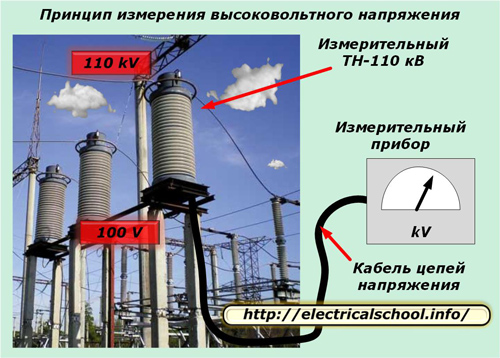
Az ilyen kábel elektromos jellemzőire fokozott követelmények vonatkoznak a feszültségátvitel minőségére.

Az elektromos berendezések korszerű védelméhez magas metrológiai mutatókkal és 0,5 vagy akár 0,2 pontossági osztályú mérőrendszerek működtetése szükséges. Ezért figyelni kell és figyelembe kell venni a rájuk kapcsolt feszültség veszteségeit. Ellenkező esetben az általuk a berendezés működésébe bevitt hiba jelentősen befolyásolhatja az összes működési jellemzőt.

Feszültségveszteség hosszú kábelvezetékekben

A hosszú kábel kialakításának sajátossága, hogy kapacitív ellenállása van a vezető magok meglehetősen szoros elrendezése és a közöttük lévő vékony szigetelőréteg miatt. Tovább tereli a kábelen áthaladó áramvektort, és megváltoztatja a nagyságát.

Az I ∙ z értékének megváltoztatásához számításba kell venni a feszültségesés kapacitív ellenállásra gyakorolt ​​hatását. Ellenkező esetben a fent leírt technológia nem változik.

A cikk példákat ad a légvezetékek és kábelek veszteségeire és feszültségesésére. Azonban minden villamosenergia-fogyasztóban megtalálhatók, beleértve a villanymotorokat, transzformátorokat, induktorokat, kondenzátortelepeket és egyéb eszközöket.

A feszültségveszteségek mértéke az egyes elektromos berendezések típusainál az üzemi feltételek tekintetében jogszabályilag szabályozott, és meghatározásuk elve minden elektromos áramkörben azonos.