Az elektronok hullámként viselkednek
A fizikusok régóta tudják, hogy a fény elektromágneses hullám. A mai napig senki sem vonja kétségbe ezt az álláspontot, hiszen a fény egyértelműen megmutatja a hullámviselkedés minden jelét: a fényhullámok átfedhetik egymást, interferenciamintázatot generálva, szétválódni is képesek, a diffrakciós idő mentén meghajolva az akadályokat.
Amikor látunk egy madarat, amely úgy jár, mint egy kacsa, úszik, mint egy kacsa, és hápog, mint egy kacsa, azt a madarat kacsának nevezzük. Tehát a fény elektromágneses hullámegy ilyen hullám fényben való viselkedésének objektíven megfigyelt jelei alapján.

A 19. és 20. század végén azonban a fizikusok a fény „részecske-hullám dualizmusáról” kezdtek beszélni. Kiderült, hogy az a tudás, hogy a fény elektromágneses hullám, nem minden, amit a tudomány a fényről tud. A tudósok egy nagyon érdekes tulajdonságot fedeztek fel a fényben.
Kiderült, hogy a fény valahogy úgy nyilvánul meg, mint egy részecskefolyam viselkedése.Megállapítást nyert, hogy a fény által hordozott energia, miután egy speciális detektor egy bizonyos ideig megszámolta, úgyis kiderül, hogy különálló (egész) darabokból áll.
Ezért vált igazzá, hogy a fény energiája diszkrét, mert mintegy egyedi részecskékből - "kvantumokból", vagyis az energia legkisebb egész részéből áll. Az ilyen egységnyi energiát (vagy kvantumot) hordozó fényrészecskét fotonnak nevezték el.
Egy foton energiáját a következő képlet határozza meg:
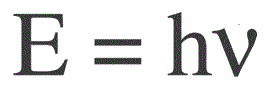
E – fotonenergia, h – Planck-állandó, v – frekvencia.
Max Planck német fizikus először kísérleti úton állapította meg a fényhullám diszkrétségének tényét, és kiszámította a h állandó értékét, amely az egyes fotonok energiájának meghatározására szolgáló képletben jelenik meg. Ez az érték a következőnek bizonyult: 6,626 * 10-34 J * s. Planck az 1900-as évek végén publikálta munkája eredményeit.

Vegyünk például egy lila sugarat. Az ilyen fény frekvenciája (f vagy v) 7,5 * 1014 Hz, a Planck-állandó (h) 6,626 * 10-34 J * s. Ez azt jelenti, hogy a foton (E) energiája, amely az ibolya színre jellemző, 5 * 10-19 J. Ez az energia olyan kis része, hogy nagyon nehéz megragadni.
Képzeljünk el egy hegyi patakot – egyetlen egységként folyik, és szabad szemmel nem lehet látni, hogy a patak valójában egyedi vízmolekulákból áll. Ma azonban tudjuk, hogy a makroszkopikus objektum – az áramlás – valójában diszkrét, azaz egyedi molekulákból áll.
Ez azt jelenti, hogy ha el tudunk helyezni egy molekulaszámlálót a patak mellé, hogy megszámolja a vízmolekulákat, amelyek a patak áramlása közben elhaladnak, akkor a detektor mindig csak egész számú vízmolekulát számol, nem részlegeset.
Hasonlóképpen, az E foton t időpontban számított teljes energiájának grafikonja mindig nem lineáris (sárga ábra), hanem lépcsőzetes (zöld ábra):
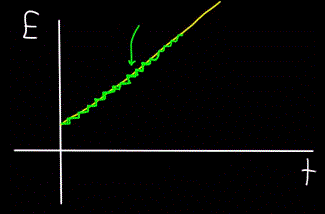
Tehát a fotonok mozognak, energiát hordoznak, ezért van lendületük. De a fotonnak nincs tömege. Akkor hogyan találhat lendületet?
Valójában a fénysebességhez közeli sebességgel mozgó objektumok esetében a klasszikus p = mv képlet egyszerűen nem alkalmazható. Hogy megértsük, hogyan lehet lendületet találni ebben a szokatlan esetben, forduljunk a speciális relativitáselmélethez:
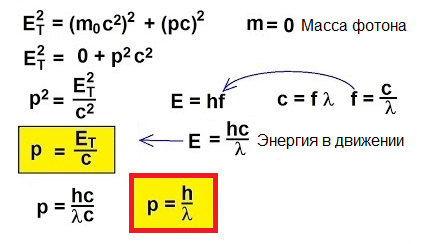
1905-ben Albert Einstein ebből a szempontból magyarázta fotoelektromos hatás… Tudjuk, hogy a fémlemezben elektronok vannak, amelyeket benne az atomok pozitív töltésű magjai vonzanak, és így a fémben maradnak. De ha egy ilyen lemezt BIZONYOS frekvenciájú fénnyel világít meg, akkor elektronokat üthet ki a lemezből.
Mintha a fény lendületes részecskefolyamként viselkedne.És bár a fotonnak nincs tömege, mégis valamilyen módon kölcsönhatásba lép a fémben lévő elektronnal, és bizonyos körülmények között a foton képes kiütni egy elektront.
Tehát ha a lemezre beeső fotonnak elegendő energiája van, akkor az elektron kiütődik a fémből, és v sebességgel kimozdul a lemezből. Az ilyen kiütött elektront fotoelektronnak nevezzük.
Mivel a kiütött elektronnak ismert m tömege van, bizonyos mv kinetikai energiája lesz.
A foton energiája, amikor a fémre hat, átalakul az elektron fémből való kilépésének energiájává (munkafunkció) és az elektron mozgási energiájává, amelynek birtokában a kiütött elektron mozogni kezd. ki a fémből, hagyva.
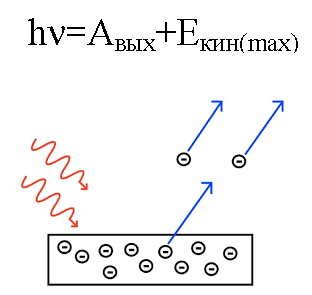
Tegyük fel, hogy egy ismert hullámhosszú foton ütközik egy fém felületével, amelynél ismert (a fémből származó elektroné) a munkafunkciója. Ebben az esetben egy adott fémből kibocsátott elektron mozgási energiája, sebessége is könnyen megtalálható.
Ha a foton energiája nem elegendő ahhoz, hogy az elektron elvégezze a munkafunkciót, akkor az elektron egyszerűen nem tud elhagyni az adott fém felületét, és a fotoelektron nem jön létre.
1924-ben francia fizikus Louis de Broglie áttörő ötletet terjesztett elő, amely szerint nemcsak a fény fotonjai, hanem maguk az elektronok is hullámként viselkedhetnek. A tudós még egy képletet is levezetett az elektron hipotetikus hullámhosszára. Ezeket a hullámokat később "de Broglie hullámoknak" nevezték el.
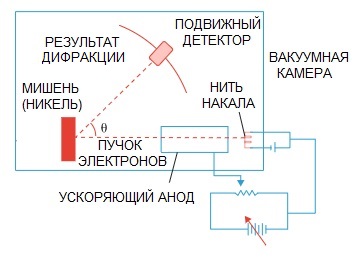
De Broglie hipotézise később beigazolódott. Clinton Davison és Lester Germer amerikai tudósok 1927-ben végzett elektrondiffrakciós fizikai kísérlete végül rámutatott az elektron hullámtermészetére.
Amikor egy elektronsugarat egy speciális atomi szerkezeten keresztül irányítottak, úgy tűnik, hogy a detektornak egymás után repülő részecskékként kellett volna rögzítenie a képet, ami logikusan elvárható lenne, ha az elektronok részecskék lennének.
De a gyakorlatban a hullámdiffrakcióra jellemző képünk van. Ráadásul ezeknek a hullámoknak a hossza teljesen összhangban van a de Broglie által javasolt koncepcióval.
Végső soron de Broglie ötlete lehetővé tette a Bohr-féle atommodell elvének magyarázatát, később pedig lehetővé tette Erwin Schrödinger számára, hogy általánosítsa ezeket az elképzeléseket, és lefektesse a modern kvantumfizika alapjait.
