Kondenzátorok párhuzamos és soros kapcsolása
Választott kondenzátorok különböző módon összekapcsolhatók. Ebben az esetben minden esetben meg lehet találni egy egyenértékű kondenzátor kapacitását, amely számos összekapcsolt kondenzátort helyettesíthet.
Egy ekvivalens kondenzátor esetén teljesül a feltétel: ha az ekvivalens kondenzátor lapjaira adott feszültség egyenlő a kondenzátorcsoport végkivezetéseire adott feszültséggel, akkor az egyenértékű kondenzátor ugyanolyan töltést halmoz fel, mint a kondenzátor csoportja. kondenzátorok.
Kondenzátorok párhuzamos csatlakoztatása
ábrán. Az 1. ábra több kondenzátor párhuzamos csatlakoztatását mutatja. Ebben az esetben az egyes kondenzátorokra adott feszültségek megegyeznek: U1 = U2 = U3 = U. Az egyes kondenzátorok lapjain lévő töltések: Q1 = C1U, B2 = C2U, B3 = C3U, és a kondenzátorból kapott töltés forrás Q = Q1 + Q2 + Q3.
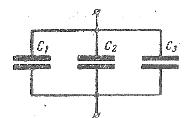
Rizs. 1. Kondenzátorok párhuzamos kapcsolásának sémája
Egy egyenértékű (ekvivalens) kondenzátor teljes kapacitása:
C = Q / U = (Q1 + Q2 + Q3) / U = C1 + C2 + C3,
vagyis ha a kondenzátorok párhuzamosan vannak kötve, a teljes kapacitás megegyezik az egyes kondenzátorok kapacitásainak összegével.

Kondenzátorok soros csatlakoztatása
Ha a kondenzátorokat sorba kötjük (3. ábra) az egyes kondenzátorok lapjain, az elektromos töltések nagysága egyenlő: Q1= Q2= Q3 = B
Valójában az áramforrásból a töltések csak a kondenzátoráramkör külső lemezeire érkeznek, és a szomszédos kondenzátorok összekapcsolt belső lapjain csak ugyanaz a töltés kerül át az egyik lemezről a másikra (elektrosztatikus indukció figyelhető meg), ezért egyenlő és különböző elektromos töltések.
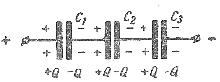
Rizs. 3. Kondenzátorok soros bekötésének sémája
Az egyes kondenzátorok lapjai közötti feszültségek sorosan kapcsolva az egyes kondenzátorok kapacitásától függenek: U1 = Q / C1, U1 = Q / C2, U1 = Q / C3 és a teljes feszültség U = U1 + U2 + U3
Egy egyenértékű (ekvivalens) kondenzátor teljes kapacitása C = Q / U = Q / (U1 + U2 + U3), amikor a kondenzátorok sorba vannak kapcsolva, a teljes kapacitás reciprok értéke megegyezik a reciprok értékek összegével az egyes kondenzátorok kapacitásától.
Az egyenértékű kapacitás képletek hasonlóak az ekvivalens vezetőképesség képletekhez.
1. példa… Három kondenzátor, amelyek kapacitása C1 = 20 mikrofarad, C2 = 25 mikrofarad és C3 = 30 mikrofarad van sorba kötve, meg kell határozni a teljes kapacitást.
A teljes kapacitást az 1 / C = 1 / C1 + 1 / C2 + 1 / C3 = 1/20 + 1/25 + 1/30 = 37/300 kifejezés adja meg, ahonnan C = 8,11 μF.
2. példa 100 kondenzátor 2 mikrofarad kapacitással párhuzamosan van csatlakoztatva.Határozza meg a teljes kapacitást. A teljes kapacitás C = 100 CK = 200 mikrofarad.

