Elektron elektromos térben

Az elektron mozgása elektromos térben az egyik legfontosabb fizikai folyamat az elektrotechnika számára. ábra Nézzük meg, hogyan történik ez vákuumban. Nézzünk először egy példát egy elektron mozgására a katódról az anódra egyenletes elektromos térben.

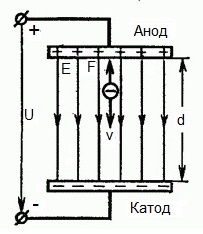
Az alábbi ábra egy olyan helyzetet mutat be, amikor elektron elhanyagolhatóan kicsi kezdeti sebességgel (nullára hajlamos) elhagyja a negatív elektródát (katódot) és belép egyenletes elektromos térbenkét elektróda között van jelen.

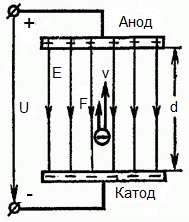
Az elektródákra állandó U feszültség vonatkozik, az elektromos tér ennek megfelelő erősségű E. Az elektródák közötti távolság d. Ebben az esetben az elektronra a tér felől egy F erő hat, amely arányos az elektron töltésével és a térerősséggel:

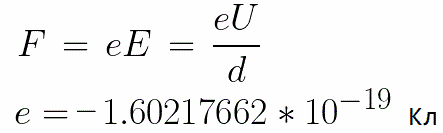
Mivel az elektron negatív töltésű, ez az erő az E térerősségvektor ellen irányul. Ennek megfelelően az elektront az elektromos tér ebbe az irányba gyorsítja.

Az elektron által tapasztalt gyorsulás arányos a rá ható F erő nagyságával és fordítottan arányos az elektron m tömegével.Mivel a mező egyenletes, az adott kép gyorsulása a következőképpen fejezhető ki:

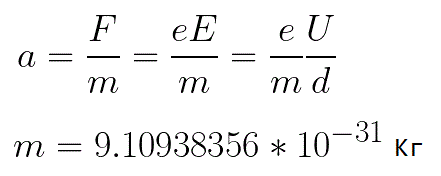
Ebben a képletben az elektron töltésének és tömegének aránya az elektron fajlagos töltése, egy olyan mennyiség, amely fizikai állandó:

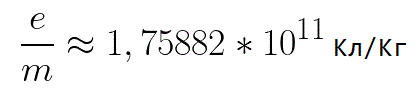
Tehát az elektron gyorsuló elektromos térben van, mert a v0 kezdősebesség iránya egybeesik a mező oldalán fellépő F erő irányával és ezért az elektron egyenletesen mozog. Ha nincs akadály, akkor az elektródák közötti d úton haladva egy bizonyos v sebességgel eléri az anódot (pozitív elektródát). Abban a pillanatban, amikor az elektron eléri az anódot, kinetikus energiája ennek megfelelően egyenlő lesz:

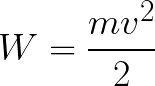
Mivel az elektront a teljes d út mentén az elektromos tér erői gyorsítják, a tér oldalán ható erő által végzett munka eredményeként nyeri el ezt a mozgási energiát. Ez a munka egyenlő:

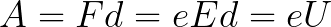
Ekkor a mezőben mozgó elektron által nyert kinetikus energia a következőképpen határozható meg:

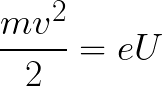
Azaz nem más, mint a térerők munkája, hogy egy elektront U potenciálkülönbségű pontok között gyorsítanak.

Ilyen helyzetekben az elektron energiájának kifejezésére célszerű olyan mértékegységet használni, mint az "elektronvolt", amely egyenlő egy elektron energiájával 1 voltos feszültség mellett. És mivel az elektrontöltés állandó, akkor 1 elektrovolt is állandó érték:

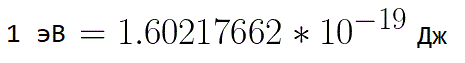
Az előző képletből könnyen meghatározhatja az elektron sebességét az út bármely pontján, amikor gyorsuló elektromos térben mozog, csak azt a potenciálkülönbséget ismerve, amelyen gyorsuláskor áthaladt:

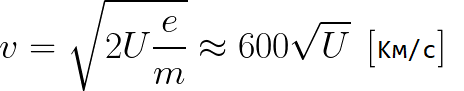
Amint látjuk, egy elektron sebessége gyorsuló térben csak az útjának végpontja és kezdőpontja közötti U potenciálkülönbségtől függ.

Képzeljük el, hogy az elektron elhanyagolható sebességgel kezd eltávolodni a katódtól, és a katód és az anód közötti feszültség 400 volt. Ebben az esetben az anód elérésének pillanatában a sebessége egyenlő lesz:

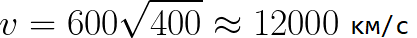
Könnyen meghatározható az is, hogy az elektronnak mennyi időre van szüksége az elektródák közötti d távolság megtételéhez. Nyugalomból egyenletesen gyorsított mozgás esetén az átlagsebesség a végsebesség fele, ekkor a gyorsított repülés ideje elektromos térben egyenlő lesz:

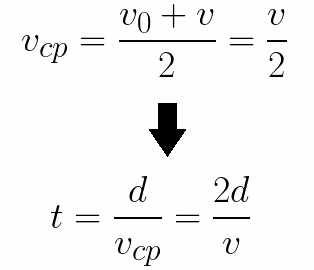
Tekintsünk most egy példát, amikor egy elektron lassuló egyenletes elektromos térben mozog, vagyis a tér iránya az előzőhöz hasonlóan történik, de az elektron az ellenkező irányba kezd el mozogni – az anódtól a katód felé.

Tegyük fel, hogy az elektron valamilyen v kezdősebességgel elhagyta az anódot, és kezdetben a katód irányába indult el. Ebben az esetben az elektronra ható F erő az elektromos tér oldaláról az E elektromos intenzitásvektor ellen irányul - a katódtól az anódig.

Elkezdi csökkenteni az elektron kezdeti sebességét, vagyis a mező lelassítja az elektront. Ez azt jelenti, hogy az elektron ilyen körülmények között egyenletesen és egyenletesen lassan mozogni kezd. A helyzet leírása a következő: "egy elektron lassuló elektromos térben mozog".

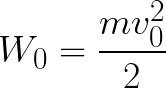
Az anódról az elektron nem nulla kinetikus energiával kezdett el mozogni, ami a lassítás során csökkenni kezd, mivel az energia most az elektronra ható mezőből ható erő leküzdésére fordítódik.

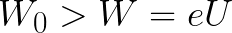
Ha az elektron kezdeti kinetikus energiája, amikor kilép az anódból, azonnal nagyobb lenne, mint az az energia, amelyet a mezőnek fel kell fordítania ahhoz, hogy felgyorsítsa az elektronnak a katódról az anódra való mozgását (mint az első példában), akkor az elektron megtesz egy d távolságot, és végül a fékezés ellenére eléri a katódot.

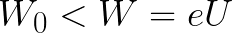
Ha az elektron kezdeti kinetikus energiája kisebb, mint ez a kritikus érték, akkor az elektron nem éri el a katódot. Egy bizonyos ponton leáll, majd egyenletesen gyorsított mozgást kezd vissza az anódhoz. Ennek eredményeként a mező visszaadja neki azt az energiát, amelyet a leállítási folyamat során elköltött.

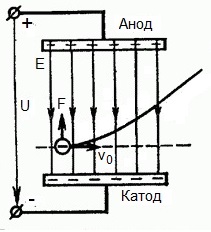
De mi van akkor, ha egy elektron v0 sebességgel repül a derékszögű elektromos tér hatástartományában? Nyilvánvaló, hogy ebben a tartományban a mező oldalán lévő erő a katódtól az anódig terjedő elektronra irányul, vagyis az E elektromos térerősség-vektor ellenében.

Ez azt jelenti, hogy most az elektronnak két mozgáskomponense van: az első - v0 sebességgel a mezőre merőlegesen, a második - egyenletesen gyorsul a tér anód felé irányuló oldaláról érkező erő hatására.

Kiderült, hogy miután a cselekvési mezőbe repült, az elektron egy parabola pályán mozog. De miután kirepült a mező hatásterületéről, az elektron tehetetlenséggel folytatja egyenletes mozgását egy egyenes pálya mentén.